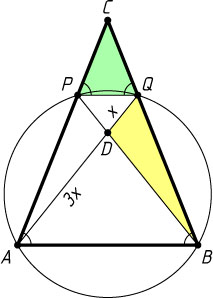
4102. Окружность, пересекающая боковые стороны AC
и CB
равнобедренного треугольника ACB
соответственно в точках P
и Q
, является описанной около треугольника ABQ
. Отрезки AQ
и BP
пересекаются в точке D
так, что AQ:AD=4:3
. Найдите площадь треугольника DQB
, если площадь треугольника PQC
равна 3.
Ответ. \frac{9}{2}
.
Указание. Рассмотрите две пары подобных треугольников ACB
и PCQ
, ADB
и QDP
.
Решение. Поскольку
\angle CPQ=180^{\circ}-\angle APQ=\angle CBA=\angle CAB=180^{\circ}-\angle BQP=\angle CQP,
то треугольник PCQ
также равнобедренный. Поэтому PQ\parallel AB
. Треугольник ADB
подобен треугольнику QDP
с коэффициентом \frac{AD}{DQ}=3
, тогда треугольник ACB
подобен треугольнику PCQ
также с коэффициентом 3.
Значит,
S_{\triangle ACB}=9\cdot S_{\triangle PCQ}=27,~S_{APQB}=S_{\triangle ACB}-S_{\triangle PCQ}=27-3=24.
Поскольку высоты треугольников AQB
и APQ
, опущенные на основания соответственно AB
и PQ
равны, то отношение площадей треугольников равно отношению оснований. Поэтому
S_{\triangle AQB}=\frac{3}{4}\cdot S_{APQB}=\frac{3}{4}\cdot24=18.
Следовательно,
S_{\triangle DQB}=\frac{DQ}{AQ}\cdot S_{\triangle AQB}=\frac{1}{4}\cdot18=\frac{9}{2}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 2004 (отделение экономики), вариант 1, № 3
Источник: Аввакумов С. Н., Бенинг В. Е. и др. Математика. Задачи вступительных экзаменов по математике. 2004. — М., 2004. — с. 15
