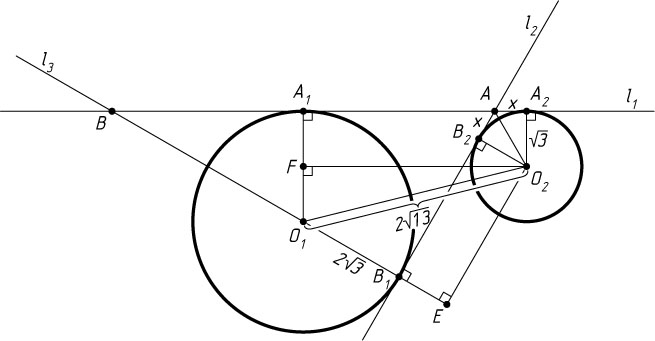
4114. Окружность C_{1}
радиуса 2\sqrt{3}
с центром O_{1}
и окружность C_{2}
радиуса \sqrt{3}
с центром O_{2}
расположены так, что O_{1}O_{2}=2\sqrt{13}
. Прямая l_{1}
касается окружностей в точках A_{1}
и A_{2}
, а прямая l_{2}
— в точках B_{1}
и B_{2}
. Окружности C_{1}
и C_{2}
лежат по одну сторону от прямой l_{1}
и по разные стороны от прямой l_{2}
, A_{1}\in C_{1}
, B_{1}\in C_{1}
, A_{2}\in C_{2}
, B_{2}\in C_{2}
, точки A_{1}
и B_{1}
лежат по разные стороны от прямой O_{1}O_{2}
. Через точку B_{1}
проведена прямая l_{3}
, перпендикулярная прямой l_{2}
. Прямая l_{1}
пересекает прямую l_{2}
в точке A
, а прямую l_{3}
— в точке B
. Найдите A_{1}A_{2}
, B_{1}B_{2}
и стороны треугольника ABB_{1}
.
Ответ. A_{1}A_{2}=7
, B_{1}B_{2}=5
, AB_{1}=6
, BB_{1}=6\sqrt{3}
, AB=12
.
Указание. Для вычисления A_{1}A_{2}
(B_{1}B_{2}
) опустите перпендикуляр из центра меньшей окружности на радиус O_{1}A_{1}
(на продолжение радиуса O_{1}B_{1}
) большей.
Обозначьте AA_{2}=AB_{2}=x
. Найдите x
из равенства AA_{1}=AB_{1}
(теорема о равенстве отрезков касательных, проведённых к окружности из одной точки).
Решение. Прямая l_{3}
перпендикулярна прямой l_{2}
и проходит через точку B_{1}
касания прямой l_{2}
с большей окружностью. Поэтому прямая l_{3}
проходит через центр O_{1}
большей окружности.
Опустим перпендикуляр O_{2}F
из центра меньшей окружности на радиус O_{1}A_{1}
большей. Тогда
O_{1}F=O_{1}A_{1}-FA_{1}=O_{1}A_{1}-O_{2}A_{2}=2\sqrt{3}-\sqrt{3}=\sqrt{3}.
По теореме Пифагора из прямоугольного треугольника O_{1}O_{2}F
находим, что
O_{2}F=\sqrt{O_{1}O_{2}^{2}-O_{1}F^{2}}=\sqrt{(2\sqrt{13})^{2}-(\sqrt{3})^{2}}=\sqrt{52-3}=\sqrt{49}=7.
Следовательно, A_{1}A_{2}=O_{2}F=7
.
Опустим перпендикуляр O_{2}E
из центра меньшей окружности на продолжение радиуса O_{1}B_{1}
большей. Тогда
O_{1}E=O_{1}B_{1}+B_{1}E=O_{1}B_{1}+O_{2}B_{2}=2\sqrt{3}+\sqrt{3}=3\sqrt{3}.
По теореме Пифагора из прямоугольного треугольника O_{1}O_{2}E
находим, что
O_{2}E=\sqrt{O_{1}O_{2}^{2}-O_{1}E^{2}}=\sqrt{(2\sqrt{13})^{2}-(3\sqrt{3})^{2}}=\sqrt{52-27}=\sqrt{25}=5.
Следовательно, B_{1}B_{2}=O_{2}E=5
.
Обозначим AA_{2}=AB_{2}=x
. Тогда
AA_{1}=A_{2}A_{1}-AA_{2}=7-x,~AB_{1}=AB_{2}+B_{2}B_{1}=x+5,
а так как AA_{1}=AB_{1}
(теорема о равенстве отрезков касательных, проведённых к окружности из одной точки), то 7-x=x+5
. Отсюда находим, что x=1
.
Следовательно, AB_{1}=x+5=1+5=6
.
Из прямоугольного треугольника AA_{2}O_{2}
находим, что
\tg\angle A_{2}AO_{2}=\frac{O_{2}A_{2}}{AA_{2}}=\frac{\sqrt{3}}{1}=\sqrt{3}.
Поэтому \angle A_{2}AO_{2}=60^{\circ}
. Поэтому
\angle BAB_{1}=180^{\circ}-2\angle A_{2}AO_{2}=180^{\circ}-120^{\circ}=60^{\circ}.
Из прямоугольного треугольника ABB_{1}
находим, что
BB_{1}=AB_{1}\cdot\tg\angle BAB_{1}=6\sqrt{3},~AB=2\cdot AB_{1}=12.
Источник: Вступительный экзамен в МФТИ. — 2001, билет 10, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 01-10-3, с. 402
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 2005 (репетиционный экзамен, февраль), вариант 2, № 4
