4121. Теорема Штейнера. Точки M
и N
лежат на прямой BC
. Прямые AM
и AN
симметричны относительно биссектрисы угла при вершине A
треугольника ABC
со сторонами AC=b
и AB=c
. Докажите, что \frac{BM\cdot BN}{CN\cdot CM}=\frac{c^{2}}{b^{2}}
. В частности, если AM
— медиана треугольника ABC
, то \frac{BN}{CN}=\frac{c^{2}}{b^{2}}
.
Указание. Примените теорему синусов к треугольникам ABM
, ABN
, ACN
и ACM
(или воспользуйтесь методом площадей).
Решение. Первый способ. Применив теорему синусов к треугольникам ABM
и ABN
, получим, что
\frac{c}{BM}=\frac{AB}{BM}=\frac{\sin\angle AMB}{\sin\angle BAM},~\frac{c}{BN}=\frac{AB}{BN}=\frac{\sin\angle ANB}{\sin\angle BAN}.
Поэтому
\frac{c^{2}}{BM\cdot BN}=\frac{c}{BM}\cdot\frac{c}{BN}=\frac{\sin\angle AMB\cdot\sin\angle ANB}{\sin\angle BAM\cdot\sin\angle BAN}.
Применив теорему синусов к треугольникам ACN
и ACM
, получим, что
\frac{b}{CN}=\frac{AC}{CN}=\frac{\sin\angle ANC}{\sin\angle CAN},~\frac{b}{CM}=\frac{AC}{CM}=\frac{\sin\angle AMC}{\sin\angle CAM}.
Поэтому
\frac{b^{2}}{CN\cdot CM}=\frac{b}{CN}\cdot\frac{b}{CM}=\frac{\sin\angle ANC\cdot\sin\angle AMC}{\sin\angle CAN\cdot\sin\angle CAM},
а так как
\sin\angle ANC=\sin\angle ANB,~\sin\angle AMC=\sin\angle AMB,
\sin\angle CAN=\sin\angle BAM,~\sin\angle CAM=\sin\angle BAN,
то
\frac{b^{2}}{CN\cdot CM}=\frac{c^{2}}{BM\cdot BN}.
Следовательно,
\frac{BM\cdot BN}{CN\cdot CM}=\frac{c^{2}}{b^{2}}.
В частности, если M
— середина BC
, то CM=BM
, поэтому \frac{BN}{CN}=\frac{c^{2}}{b^{2}}
.
Второй способ. У треугольников ABN
и ABM
общая высота, проведённая из вершины A
, поэтому \frac{S_{\triangle ABN}}{S_{\triangle ACM}}=\frac{BN}{CM}
. С другой стороны, так как \angle BAN=\angle CAM
, то
\frac{S_{\triangle ABN}}{S_{\triangle ACM}}=\frac{\frac{1}{2}AB\cdot AN\sin\angle BAN}{\frac{1}{2}AC\cdot AM\sin\angle CAM}=\frac{AB\cdot AN}{AC\cdot AM}.
Значит, \frac{BN}{CM}=\frac{AB\cdot AN}{AC\cdot AM}
. Аналогично \frac{BM}{CN}=\frac{AB\cdot AM}{AC\cdot AN}
. Перемножив эти равенства, получим, что
\frac{BM\cdot BN}{CN\cdot CM}=\frac{AB^{2}}{AC^{2}}=\frac{c^{2}}{b^{2}}.
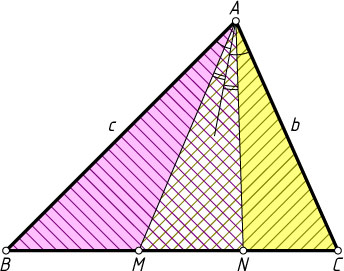
Примечание. 1. Пусть AM
— медиана треугольника ABC
, а прямая AN
симметрична прямой AM
относительно биссектрисы угла A
(точка N
лежит на отрезке BC
). Тогда отрезок AN
называется симедианой треугольника ABC
(иногда симедианой называют луч AN
).
Из доказанной теоремы следует, что симедиана треугольника разбивает его сторону на отрезки, пропорциональные квадратам двух других сторон. Верно и обратное, если точка M
, лежащая на стороне BC
треугольника ABC
, разбивает эту сторону на отрезки, пропорциональные квадратам двух других сторон, то AM
— симедиана треугольника
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 119
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 94
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.123, с. 121
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.149, с. 119
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 15, с. 183
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 3.9, с. 32
