4149. В треугольнике ABC
с углом \angle B=50^{\circ}
и стороной BC=3
на высоте BH
взята такая точка D
, что \angle ADC=130^{\circ}
и AD=\sqrt{3}
. Найдите угол между прямыми AD
и BC
, а также \angle CBH
.
Ответ. 90^{\circ}
, 20^{\circ}
.
Указание. Пусть точка D'
симметрична точке D
относительно прямой AC
. Тогда около четырёхугольника ABCD'
можно описать окружность.
Решение. Пусть точка D'
симметрична точке D
относительно прямой AC
. Тогда
\angle ABC+\angle AD'C=\angle ABC+\angle ADC=50^{\circ}+130^{\circ}=180^{\circ}.
Значит, около четырёхугольника ABCD'
можно описать окружность.
Пусть продолжение отрезка AD
пересекает прямую BC
в точке P
. Обозначим \angle CBH=\alpha
. Тогда
\angle DAH=\angle DAC=\angle CAD'=\angle CBD'=\alpha,
\angle BDP=\angle ADH=90^{\circ}-\angle DAC=90^{\circ}-\alpha.
Следовательно,
\angle DPB=180^{\circ}-\angle DBP-\angle BDP=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ}.
Из подобия прямоугольных треугольников AHD
и BHC
следует, что
\frac{\sqrt{3}}{3}=\frac{AD}{BC}=\frac{AH}{BH}=\tg\angle ABH.
Значит, \angle ABH=30^{\circ}
. Следовательно,
\angle CBH=\angle ABC-\angle ABH=50^{\circ}-30^{\circ}=20^{\circ}.
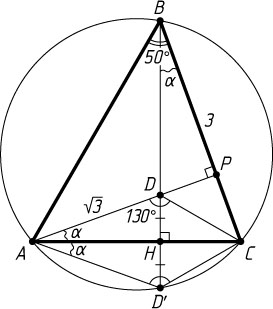
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2003 (май), вариант 1, № 3
