4164. Дан треугольник ABC
. Окружность \omega
касается описанной окружности треугольника ABC
в точке A
, пересекает сторону AB
в точке K
, а также пересекает сторону BC
. Касательная CL
к окружности \omega
такова, что отрезок KL
пересекает сторону BC
в точке T
. Докажите, что отрезок BT
равен по длине касательной из точки B
к \omega
.
Указание. Треугольники BTA
и BKT
подобны.
Решение. Пусть M
— вторая точка пересечения окружности \omega
с отрезком AC
. При гомотетии с центром A
окружность \omega
переходит в описанную окружность треугольника ABC
, точка K
— в точку B
, а точка M
— в точку C
, значит, прямая KM
переходит при этом в параллельную ей прямую BC
. Тогда \angle AMK=\angle ACB=\angle ACT
.
Четырёхугольник AMLK
вписан в окружность \omega
, поэтому \angle AMK=\angle ALK=\angle ALT
, значит, \angle ALT=\angle ACT
, т. е. отрезок AT
виден из точек L
и C
, лежащих по одну сторону от прямой AT
, под одним и тем же углом. Следовательно, точки A
, T
, L
и C
лежат на одной окружности. Вписанные в эту окружность углы ALC
и ATC
опираются на одну и ту же дугу, поэтому \angle ATC=\angle ALC
. Из теоремы об угле между касательной о хордой \angle ALC=\angle AKL=\angle AKT
, значит, \angle AKT=\angle ATC
, поэтому
\angle BKT=180^{\circ}-\angle AKT=180^{\circ}-\angle ATC=\angle ATB.
Тогда треугольники BTA
и BKT
подобны по двум углам, поэтому \frac{BT}{BK}=\frac{BA}{BT}
, откуда BT^{2}=BK\cdot BA
. С другой стороны, квадрат касательной, проведённой из точки B
к окружности \omega
, также равен BK\cdot BA
. Отсюда следует утверждение задачи.
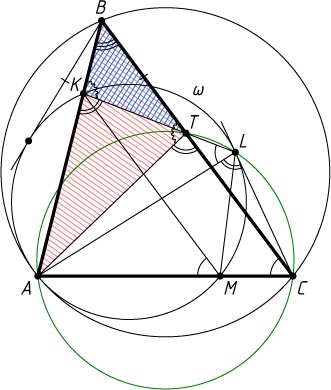
Автор: Скробот Д.
Источник: Всероссийская олимпиада школьников. — 2005-06, XXXII, заключительный этап, 9 класс
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 742, с. 95
