4165. Окружность \omega
касается равных сторон AB
и AC
равнобедренного треугольника ABC
и пересекает сторону BC
в точках K
и L
. Отрезок AK
пересекает \omega
второй раз в точке M
. Точки P
и Q
симметричны точке K
относительно точек B
и C
соответственно. Докажите, что описанная окружность треугольника PMQ
касается окружности \omega
.
Указание. Докажите, что точка M
— центр гомотетии окружности, описанной около треугольника PQM
, и окружности, описанной около треугольника DEM
.
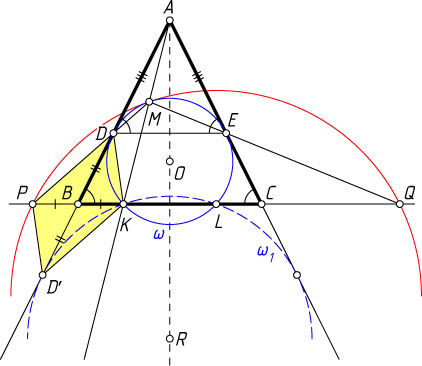
Решение. Пусть D
и E
— точки касания окружности со сторонами AB
и AC
. Тогда AD=AE
, поэтому углы при основании DE
равнобедренного треугольника ADE
равны углам при основании BC
равнобедренного треугольника ABC
, значит, DE\parallel BC
.
При гомотетии с центром A
и коэффициентом \frac{AK}{AM}
точка M
переходит в точку K
, окружность \omega
— в некоторую окружность \omega_{1}
, проходящую через точку K
, точка D
касания прямой AB
с окружностью \omega
— в точку D'
касания прямой AD
с окружностью \omega_{1}
, отрезок MD
— в параллельный ему отрезок KD'
.
По теореме о касательной и секущей
BD^{2}=BL\cdot BK=BD'^{2},
значит, BD=BD'
, а так как BK=BP
, то четырёхугольник DKD'P
— параллелограмм, поэтому DP\parallel KD'
. Следовательно, точки M
, D
и P
лежат на одной прямой. Аналогично, точки M
, E
и Q
лежат на одной прямой.
При гомотетии с центром M
, переводящей точку D
в точку P
, точка E
переходит в точку Q
, треугольник DME
— в треугольник PMQ
, а окружность, описанная около треугольника DME
— в окружность, описанную около треугольника PMQ
. Следовательно, эти две окружности касаются в точке M
.
Автор: Филимонов В. П.
Источник: Всероссийская олимпиада школьников. — 2005-06, XXXII, заключительный этап, 10 класс
Источник: Журнал «Квант». — 2006, № 5, с. 16, М2019; 2007, № 2, с. 17, М2019
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 748, с. 96
