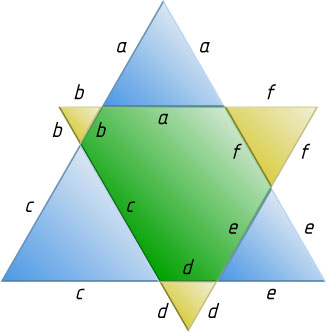
4169. Два равносторонних треугольника со сторонами 12 и 15 расположены так, что их стороны соответственно параллельны (см.рис.). Найдите периметр образовавшегося шестиугольника.

Ответ. 27.
Решение. Пусть a
, b
, c
, d
, e
и f
— стороны образовавшихся равносторонних треугольников. Тогда a+b+c=15
и d+e+f=12
. Следовательно, периметр шестиугольника равен
a+b+c+d+e+f=(a+b+c)+(d+e+f)=15+12=27.
Источник: Московская математическая олимпиада. — 2004, LXVII, окружной тур, 8 класс

