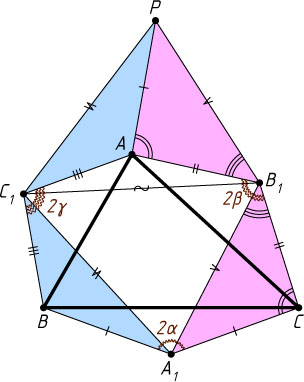
4183. На сторонах произвольного треугольника ABC
внешним образом построены равнобедренные треугольники с углами 2\alpha
, 2\beta
и 2\gamma
при вершинах A_{1}
, B_{1}
и C_{1}
, причём \alpha+\beta+\gamma=180^{\circ}
. Докажите, что углы треугольника A_{1}B_{1}C_{1}
равны \alpha
, \beta
и \gamma
.
Решение. Пусть \angle AC_{1}B=2\gamma
, \angle AB_{1}C=2\beta
, \angle BA_{1}C=2\alpha
. Сумма углов шестиугольника AC_{1}BA_{1}CB_{1}
равна 180^{\circ}(6-2)=720^{\circ}
, а так как \angle BA_{1}C+\angle AB_{1}C+\angle AC_{1}B=2\alpha+2\beta+2\gamma=360^{\circ}
, то
\angle B_{1}AC_{1}+\angle A_{1}BC_{1}+\angle B_{1}CA_{1}=720^{\circ}-360^{\circ}=360^{\circ}.
Пусть при повороте вокруг точки C_{1}
, переводящем точку B
в точку A
, точка A_{1}
перешла в некоторую точку P
. Тогда треугольник PAC_{1}
равен треугольнику A_{1}BC_{1}
, а так как AP=BA_{1}=CA_{1}
, AB_{1}=CB_{1}
и
\angle PAB_{1}=360^{\circ}-\angle PAC_{1}-B_{1}AC_{1}=360^{\circ}-\angle A_{1}BC_{1}-B_{1}AC_{1}=
=360^{\circ}-(360^{\circ}-\angle A_{1}CB_{1})=\angle A_{1}CB_{1},
то треугольники PAB_{1}
и A_{1}CB_{1}
равны по двум сторонам и углу между ними, поэтому PB_{1}=A_{1}B_{1}
. Значит, треугольники PB_{1}C_{1}
и A_{1}B_{1}C_{1}
равны по трём сторонам. Тогда
\angle PB_{1}A=\angle CB_{1}A_{1},~\angle PB_{1}A_{1}=\angle PB_{1}A+\angle AB_{1}A_{1}=\angle CB_{1}A_{1}+\angle AB_{1}A_{1}=\angle AB_{1}C=2\beta.
Следовательно,
\angle A_{1}B_{1}C_{1}=\frac{1}{2}\angle PB_{1}A_{1}=\frac{1}{2}\angle AB_{1}C=\beta.
Аналогично,
\angle B_{1}A_{1}C_{1}=\alpha,~\angle A_{1}C_{1}B_{1}=\gamma.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.47
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.48, с. 16
