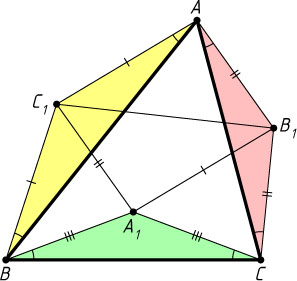
4184. На сторонах треугольника ABC
как на основаниях построены равнобедренные подобные треугольники AB_{1}C
и AC_{1}B
внешним образом и BA_{1}C
внутренним образом. Докажите, что AB_{1}A_{1}C_{1}
— параллелограмм.
Решение. Треугольник A_{1}BC_{1}
подобен треугольнику ABC
, так как \frac{BC_{1}}{AB}=\frac{BA_{1}}{BC}
и
\angle A_{1}BC_{1}=\angle ABA_{1}+\angle ABC_{1}=\angle ABA_{1}+\angle CBA_{1}=\angle ABC.
Аналогично, треугольник B_{1}A_{1}C
также подобен треугольнику ABC
. Значит, треугольники A_{1}BC_{1}
и B_{1}A_{1}C
подобны, а так как их соответствующие стороны BA_{1}
и CA_{1}
равны, то треугольники A_{1}BC_{1}
и B_{1}A_{1}C
равны. Тогда A_{1}B_{1}=BC_{1}=AC_{1}
и A_{1}C_{1}=CB_{1}=AB_{1}
, т. е. противоположные стороны четырёхугольника AB_{1}A_{1}C_{1}
попарно равны. Следовательно, AB_{1}A_{1}C_{1}
— параллелограмм.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.48
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.49, с. 16
