4189. Докажите, что проекции основания высоты треугольника на стороны, её заключающие, и на две другие высоты лежат на одной прямой.
Решение. Пусть AA_{1}
, BB_{1}
и CC_{1}
— высоты треугольника ABC
, K
и N
— проекции точки B_{1}
на AB
и BC
, L
и M
— проекции точки B_{1}
на AA_{1}
и CC_{1}
соответственно.
Прямые B_{1}K
и CC_{1}
параллельны, так как они перпендикулярны одной и той же прямой AB
, поэтому треугольник AB_{1}K
подобен треугольнику ACC_{1}
. Аналогично, треугольник AB_{1}L
подобен треугольнику ACA_{1}
. Значит, \frac{KB_{1}}{CC_{1}}=\frac{AB_{1}}{AC}=\frac{LB_{1}}{A_{1}C}
, а так как KB_{1}\parallel CC_{1}
, то треугольник KLB_{1}
подобен треугольнику C_{1}A_{1}C
. Тогда
\angle A_{1}C_{1}C=\angle LKB_{1},~\angle A_{1}C_{1}A=90^{\circ}+\angle A_{1}C_{1}C=90^{\circ}+\angle LKB_{1}=\angle LKA.
Следовательно, KL\parallel A_{1}C_{1}
.
Пусть H
— точка пересечения высот треугольника ABC
. Треугольник BC_{1}H
подобен треугольнику BKB_{1}
, а треугольник BNB_{1}
— треугольнику BA_{1}H
, поэтому \frac{BC_{1}}{BK}=\frac{BH}{BB_{1}}=\frac{BA_{1}}{BN}
, значит, KN\parallel A_{1}C_{1}
, а так как KL\parallel A_{1}C_{1}
, то точки K
, L
и N
лежат на одной прямой. Аналогично, точка M
лежит на этой же прямой.
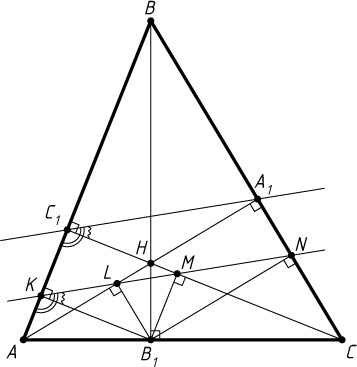
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.63
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.64, с. 18
