4195. В равностороннем (неправильном) пятиугольнике ABCDE
угол ABC
вдвое больше угла DBE
. Найдите величину угла ABC
.
Ответ. 60^{\circ}
.
Указание. Докажите, что AE\parallel CD
.
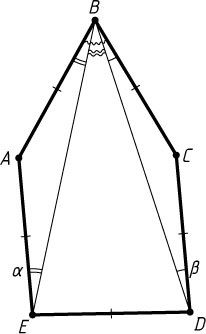
Решение. Пусть углы при основании BE
равнобедренного треугольника ABE
равны \alpha
, а углы при основании BD
равнобедренного треугольника BCD
равны \beta
. Из условия задачи следует, что \alpha+\beta=\angle DBE
. Тогда
\angle AED+\angle CDE=(\alpha+\angle BED)+(\beta+\angle BDE)=(\alpha+\beta)+(\angle BED+\angle BDE)=
=\angle DBE+(180^{\circ}-\angle DBE)=180^{\circ}.
Следовательно, AE\parallel CD
, а так как AE=CD
, то четырёхугольник ACDE
— параллелограмм, поэтому AC=DE=AB=BC
. Значит, треугольник ABC
— равносторонний, и \angle ABC=60^{\circ}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.44
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.48, с. 156
