4199. На сторонах произвольного остроугольного треугольника ABC
как на диаметрах построены окружности. При этом образуется три «внешних» криволинейных треугольника и один «внутренний» (см. рис.). Докажите, что если из суммы площадей «внешних» треугольников вычесть площадь «внутреннего», то получится удвоенная площадь треугольника ABC
.
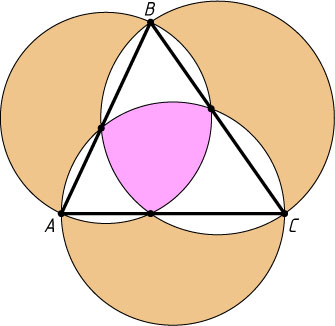
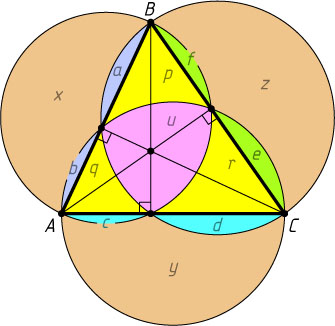
Решение. Рассматриваемые окружности проходят через основания высот треугольника ABC
, поэтому точки их пересечения лежат на сторонах треугольника. Пусть x
, y
, z
и u
— площади рассматриваемых криволинейных треугольников; a
, b
, c
, d
, e
и f
— площади сегментов, отсекаемых от окружностей сторонами треугольника; p
, q
и r
— площади частей треугольника ABC
, лежащих вне внутреннего криволинейного треугольника. Тогда
x+(a+b)=u+p+q+(c+f),
y+(c+d)=u+q+r+(e+b),
z+(e+f)=u+r+p+(a+d).
Складывая эти равенства, получаем, что
x+y+z=2(p+q+r+u)+u,
откуда
(x+y+z)-u=2(p+q+r+u)=2S_{\triangle ABC}.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.41
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.40, с. 61

