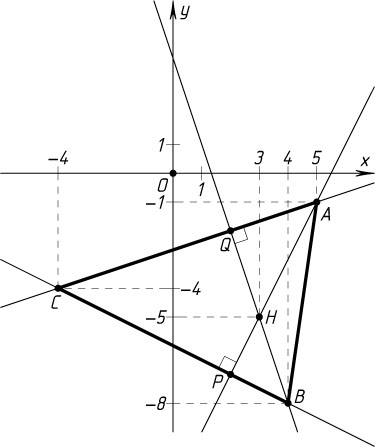
4247. Даны точки A(5;-1)
, B(4;-8)
, C(-4;-4)
. Найдите координаты точки пересечения высот треугольника ABC
.
Ответ. (3;-5)
.
Указание. Применив условие перпендикулярности двух прямых (k_{1}\cdot k_{2}=-1
), найдите уравнения прямых, на которых лежат две высоты треугольника. Затем найдите координаты точки пересечения этих прямых, решив соответствующую систему уравнений.
Решение. Найдём уравнение прямой BC
по двум точкам:
\frac{y-(-8)}{-4-(-8)}=\frac{x-4}{-4-4},~\mbox{или}~y=-\frac{1}{2}x-6.
Тогда её угловой коэффициент k_{1}=-\frac{1}{2}
. Если k_{2}
— угловой коэффициент прямой, содержащей высоту AP
, то k_{1}\cdot k_{2}=-1
. Поэтому
k_{2}=-\frac{1}{k_{1}}=2.
Уравнение прямой, содержащей высоту AP
треугольника ABC
, найдём по точке A(5;-1)
и угловому коэффициенту k_{2}=2
:
y+1=2(x-5),~\mbox{или}~y=2x-11.
Найдём уравнение прямой AC
по двум точкам:
\frac{y-(-1)}{-4-(-1)}=\frac{x-5}{-4-5},~\mbox{или}~y=\frac{1}{3}x-\frac{8}{3}.
Тогда её угловой коэффициент k_{3}=\frac{1}{3}
. Если k_{4}
— угловой коэффициент прямой, содержащей высоту BQ
, то k_{4}\cdot k_{3}=-1
. Поэтому
k_{4}=-\frac{1}{k_{3}}=-3.
Уравнение прямой, содержащей высоту BQ
треугольника ABC
, найдём по точке B(4;-8)
и угловому коэффициенту k_{4}=-3
:
y+8=-3(x-4),~\mbox{или}~y=-3x+4.
Координаты точки H
пересечения высот треугольника ABC
найдём, решив систему уравнений, задающих прямые AP
и BQ
:
\syst{y=2x-11\\y=-3x+4.\\}
Получим: x=3
, y=-5
.