4288. Докажите, что внутри остроугольного треугольника существует такая точка, что основания перпендикуляров, опущенных из неё на стороны, являются вершинами равностороннего треугольника.
Указание. Пусть ABC
— данный треугольник. Постройте внутри произвольного равностороннего треугольника точку, из которой его стороны видны под углами, равными 180^{\circ}-\angle A
, 180^{\circ}-\angle B
и 180^{\circ}-\angle C
.
Решение. Пусть внутри нашего треугольника ABC
есть такая точка Q
, о которой говорится в задаче. Обозначим проекции точки Q
на стороны AB
, BC
и AC
через M
, N
и P
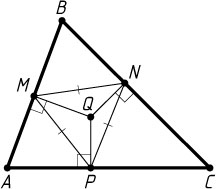
соответственно (рис. 1). Тогда
\angle MQP=180^{\circ}-\angle A,~\angle MQN=180^{\circ}-\angle B,~\angle NQP=180^{\circ}-\angle C.
По условию углы A
, B
и C
— острые, поэтому углы MQP
, MQN
и NQP
— тупые, причём их сумма равна 360^{\circ}
. Треугольник MNQ
— равносторонний (по предположению).
Рассмотрим теперь произвольный равносторонний треугольник XYZ
и найдём внутри него такую точку O
, для которой углы XOY
, YOZ
и XOZ
имеют заданную величину, а именно, равны углам MQP
, MQN
и NQP
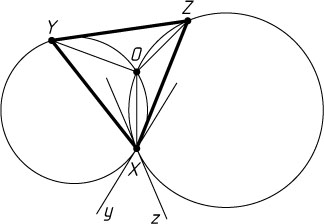
соответственно (рис. 2).
В той полуплоскости относительно прямой XY
, в которой не лежит точка Z
, построим дугу, из каждой точки которой отрезок XY
виден под углом, равным углу A
данного треугольника. Тогда из каждой точки дополнительной к ней дуги, отрезок XY
будет виден под углом, равным 180^{\circ}-\angle A
.
Аналогично получим дуги, из которых отрезки XZ
и YZ
видны под углами, равными 180^{\circ}-\angle B
и 180^{\circ}-\angle C
соответственно.
Каждые две (дополнительные) дуги пересекаются. Докажем, что пересекаются дуги XY
и XZ
. Проведём через точку X
касательные y
и z
к дугам соответственно XY
и XZ
. Острый угол между y
и отрезком XY
обозначим через \alpha
, а острый угол между z
и отрезком XZ
— через \beta
. Из теоремы об угле между касательной и хордой следует, что \alpha=\angle A
и \beta=\angle B
, причём \alpha+\beta\gt90^{\circ}
, так как угол C
— острый. Значит, \alpha+\beta\gt60^{\circ}
. Отсюда следует, что дуги XY
и XZ
пересекаются в некоторой точке O
внутри угла YXZ
, а так как сумма углов MQP
, NQP
и MQN
равна 360^{\circ}
, то через точку O
проходит и внутренняя дуга ZY
.
Итак, существует, и притом только одна такая точка O
, из которой стороны треугольника XYZ
видны под заданными углами.
Теперь решим нашу задачу на построение. Через точки X
, Y
, Z
проведём прямые, перпендикулярные отрезкам OX
, OY
и OZ
. Точки пересечения этих прямых являются вершинами треугольника, подобного данному треугольнику ABC
(у данного и построенного треугольника соответственно равные углы). Разделим стороны треугольника ABC
в тех же отношениях, в которых точки X
, Y
и Z
делят соответствующие стороны построенного треугольника. Точки деления и будут искомыми точками M
, N
и P
.
Автор: Васильев Н. Б.
Источник: Турнир городов. — 1995-1996, XVII, осенний тур, младшие классы, основной вариант

