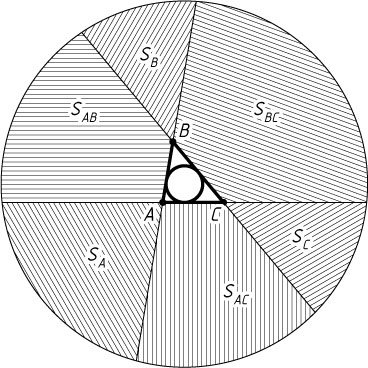
4298. Учитель продиктовал классу задание, которое каждый ученик выполнил в своей тетради. Вот это задание: «Нарисуйте две концентрические окружности радиусов 1 и 10. К малой окружности проведите три касательные так, чтобы их точки пересечения A
, B
и C
лежали внутри большой окружности. Измерьте площадь S
треугольника ABC
и площади S_{A}
, S_{B}
и S_{C}
трёх образовавшихся криволинейных треугольников с вершинами в точках A
, B
и C
. Найдите S_{A}+S_{B}+S_{C}-S
».
Докажите, что у всех учеников (если они правильно выполнили задание) получились одинаковые результаты.
Решение. Если некоторая хорда делит площадь круга на части с площадями P
и Q
, то равная ей хорда делит площадь круга на такие же части P
и Q
. Заметим, что отрезки касательных к малой окружности, заключённые внутри большой, равны между собой, так как хорды, равноудалённые от центра окружности, равны.
Пусть S_{AB}
, S_{BC}
, S_{AC}
— площади трёх криволинейных четырёхугольников со сторонами AB
, BC
и AC
соответственно. Обозначим
\syst{S_{A}+S_{B}+S_{AB}=\sigma\\S_{A}+S_{AC}+S_{C}=\sigma\\S_{BC}+S_{B}+S_{C}=\sigma,}~~~\syst{S+S_{BC}+S_{AC}+S_{C}=\Sigma\\S+S_{A}+S_{AC}+S_{AB}=\Sigma\\S+S_{BC}+S_{B}+S_{AB}=\Sigma.}
Сложив почленно равенства первой системы, получим:
2(S_{A}+S_{B}+S_{C})+(S_{BC}+S_{AC}+S_{AB})=3\sigma.
Сложив почленно равенства второй системы, получим:
3S+(S_{A}+S_{B}+S_{C})+2(S_{BC}+S_{AC}+S_{AB})=3\Sigma.
Первое из полученных равенств умножим почленно на 2 и вычтем из результата второе. Получим
3(S_{A}+S_{B}+S_{C})-3S=6\sigma-3\Sigma.
Поскольку \sigma
и \Sigma
зависят только от радиусов окружностей, то величина (S_{A}+S_{B}+S_{C})-S
также зависит только от радиусов окружностей.
Автор: Толпыго А. К.
Источник: Турнир городов. — 1985-1986, VII, осенний тур, младшие классы, основной вариант
