4307. Из точки M
внутри треугольника опущены перпендикуляры на высоты. Оказалось, что отрезки высот от вершин до оснований этих перпендикуляров равны между собой. Докажите, что в этом случае они равны диаметру вписанной в треугольник окружности.
Указание. Примените метод площадей или проведите через вершины данного треугольника прямые, параллельные противоположным сторонам.
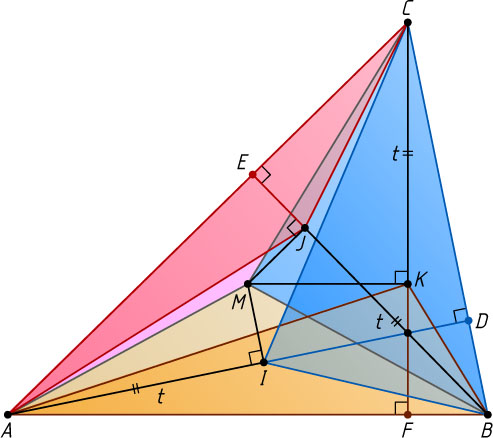
Решение. Первый способ. Пусть I
, J
и K
— проекции точки M
на высоты соответственно AD
, BE
и CF
треугольника ABC
(рис. 1). Обозначим AI=BJ=CK=t
.
Вычислим площадь S
треугольника ABC
двумя способами: с одной стороны
S_{\triangle ABC}=\frac{1}{2}AB\cdot CF=\frac{1}{2}BC\cdot AD=\frac{1}{2}AC\cdot BE,
с другой стороны, так как
S_{\triangle AMB}=S_{\triangle AKB},~S_{\triangle BMC}=S_{\triangle BIC},~S_{\triangle AMC}=S_{\triangle AJC}
(у соответствующих треугольников равные основания и равные высоты), то
S=S_{\triangle AMB}+S_{\triangle BMC}+S_{\triangle AMC}=
=S_{\triangle AKB}+S_{\triangle BIC}+S_{\triangle AJC}=
=\frac{1}{2}AB\cdot FK+\frac{1}{2}BC\cdot DI+\frac{1}{2}AC\cdot EJ.
Поэтому
S=\frac{1}{2}AB(CF-CK)+\frac{1}{2}BC(AD-AI)+\frac{1}{2}AC(BE-BJ)=
=\frac{1}{2}AB\cdot CF+\frac{1}{2}BC\cdot AD+\frac{1}{2}AC\cdot BE-\left(\frac{1}{2}AB\cdot CK+\frac{1}{2}BC\cdot AI+\frac{1}{2}AC\cdot BJ\right)=
=S+S+S-\frac{1}{2}(AB\cdot t+BC\cdot t+AC\cdot t)=
=3S-\frac{1}{2}(AB+BC+AC)t.
Отсюда находим, что
S=\frac{1}{4}(AB+BC+AC)t.
В то же время,
S_{\triangle ABC}=\frac{1}{2}(AB+BC+AC)r,
где r
— радиус вписанной окружности треугольника ABC
. Следовательно, t=2r
.
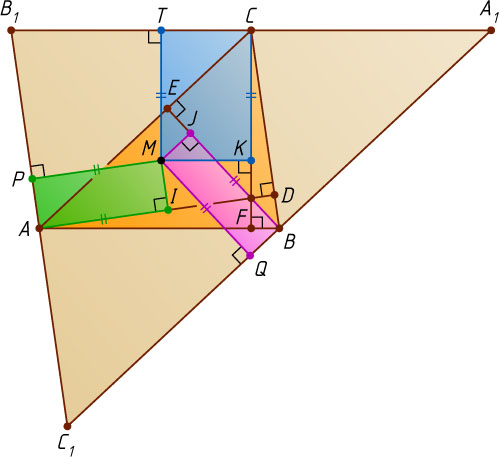
Второй способ. (Д. Макаров.) Пусть I
, J
и K
— проекции точки M
на высоты соответственно AD
, BE
и CF
треугольника ABC
(рис. 2). Через вершины A
, B
и C
проведём прямые, параллельные сторонам BC
, AC
и AB
соответственно. Получим треугольник A_{1}B_{1}C_{1}
, подобный треугольнику ABC
с коэффициентом 2. Из точки M
опустим перпендикуляры MP
, MQ
и MT
на стороны B_{1}C_{1}
, A_{1}C_{1}
и A_{1}B_{1}
соответственно. Тогда MP=IA
, MQ=JB
и MT=KC
, а так как IA=JB=KC
, то MP=MQ=MT
.
Таким образом, точка M
, лежащая внутри треугольника A_{1}B_{1}C_{1}
, равноудалена от его сторон, значит, M
— центр вписанной окружности треугольника A_{1}B_{1}C_{1}
, а MP=MQ=MT
— радиусы этой окружности.
Треугольник ABC
подобен треугольнику A_{1}B_{1}C_{1}
с коэффициентом \frac{1}{2}
, поэтому диаметр вписанной окружности треугольника ABC
равен радиусу вписанной окружности треугольника A_{1}B_{1}C_{1}
. Отсюда следует утверждение задачи.
Примечание. Если под проекцией точки M
на высоту подразумевать проекцию на прямую, содержащую высоту, то такому условию удовлетворяют ещё три точки — центры вневписанных окружностей треугольника A_{0}B_{0}C_{0}
. См. Квант, 1988, N2, с.26, задача М1087.
Автор: Джафаров А. Х.
Источник: Турнир городов. — 1987-1988, IX, осенний тур, старшие классы, основной вариант
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.5, с. 105
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.5, с. 102
Источник: Журнал «Квант». — 1988, № 2, с. 26, М1087; 1988, № 6, с. 28, М1087
Источник: Задачник «Кванта». — 1988, № 2, с. 26, М1087

