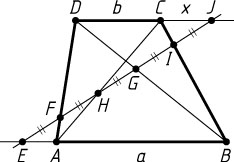
4309. При каком отношении оснований трапеции существует прямая, на которой шесть точек пересечения с диагоналями, боковыми сторонами и продолжениями оснований трапеции высекают пять равных отрезков?
Ответ. 1:2
.
Решение. Пусть указанная прямая пересекает продолжение меньшего основания AB
трапеции ABCD
, в точке E
, боковую сторону AD
— в точке F
, диагональ BD
— в точке G
, диагональ AC
— в точке H
, боковую сторону BC
— в точке I
, продолжение основания CD
— в точке J
.
Обозначим AB=a
, CD=b
, CJ=x
. Из подобия треугольников IBE
и ICJ
находим, что
BE=CJ\cdot\frac{IE}{IJ}=4x,
а из подобия треугольников HAE
и HCJ
—
AE=CJ\cdot\frac{HE}{HJ}=\frac{2}{3}x.
Из равенства
4x=BE=AE+AB=\frac{2}{3}x+a
следует, что a=\frac{10}{3}x
.
Из подобия треугольников GBE
и GDJ
следует, что
x+b=DJ=BE\cdot\frac{GJ}{GE}=4x\cdot\frac{2}{3}=\frac{8}{3}x.
Значит, b=\frac{5}{3}x
. Следовательно,
\frac{AB}{CD}=\frac{a}{b}=\frac{\frac{10}{3}x}{\frac{5}{3}x}=2.
Источник: Турнир городов. — 1987-1988, IX, весенний тур, старшие классы, основной вариант
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.21, с. 47
