4320. Даны две окружности, лежащие одна вне другой. Пусть A_{1}
и A_{2}
— наиболее удалённые друг от друга точки пересечения этих окружностей с их линией центров, так что A_{1}
лежит на первой окружности, а A_{2}
— на второй. Из точки A_{1}
проведены два луча, касающиеся второй окружности, и построен круг K_{1}
, касающийся этих лучей и первой окружности изнутри. Из точки A_{2}
проведены два луча, касающиеся первой окружности, и построен круг K_{2}
, касающийся этих лучей и второй окружности изнутри. Докажите, что круги K_{1}
и K_{2}
равны.
Указание. Используя подобие треугольников, выразите радиусы кругов K_{1}
и K_{2}
через радиусы данных окружностей и расстояние A_{1}A_{2}
.
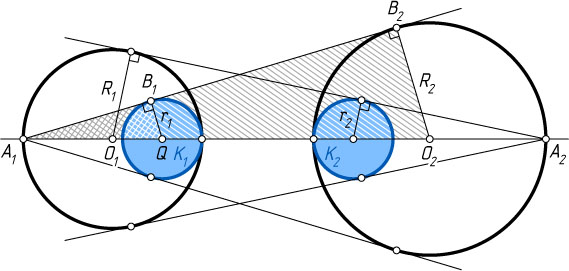
Решение. Пусть R_{1}
и R_{2}
— радиусы первой и второй окружностей соответственно, O_{1}
и O_{2}
— центры этих окружностей, B_{1}
— точка касания с кругом K_{1}
луча с началом в точке A_{1}
, касающегося второй окружности в точке B_{2}
, A_{1}A_{2}=d
, r_{1}
— радиус круга K_{1}
с центром Q
, r_{2}
— радиус круга K_{2}
.
Из подобия треугольников A_{1}B_{1}Q
и A_{1}B_{2}O_{2}
следует, что
\frac{QB_{1}}{A_{1}Q}=\frac{O_{2}B_{2}}{A_{1}O_{2}},~\mbox{или}~\frac{r_{1}}{2R_{1}-r_{1}}=\frac{R_{2}}{d-R_{2}},~\mbox{или}~r_{1}d-r_{1}R_{2}=2R_{1}R_{2}-r_{1}R_{2}.
Отсюда находим, что
r_{1}=\frac{2R_{1}R_{2}}{d}.
Точно так же находим, что
r_{2}=\frac{2R_{1}R_{2}}{d}.
Следовательно, r_{1}=r_{2}
.
Источник: Турнир городов. — 1989-1990, XI, весенний тур, младшие классы, тренировочный вариант
