4325. Для каждой точки C
полуокружности с диаметром AB
(C
отлична от A
и B
) на сторонах AC
и BC
треугольника ABC
построены вне треугольника квадраты. Найдите геометрическое место середин отрезков, соединяющих их центры.
Ответ. Полуокружность.
Указание. Пусть D
— середина полуокружности. Докажите, что середина отрезка с концами в центрах квадратов совпадает с серединой отрезка CD
.
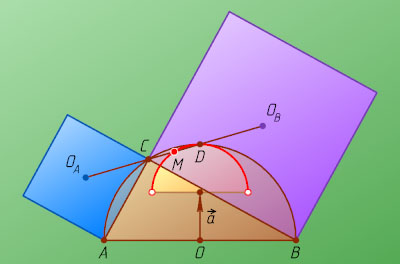
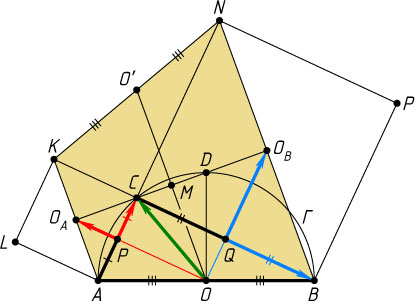
Решение. Первый способ. Пусть O
— центр, а D
— середина полуокружности \Gamma
; O_{A}
и O_{B}
— центры квадратов ACKL
и BCNP
соответственно (рис. 1). Предположим, что точка C
не совпадает с D
.
Поскольку \angle KAN=\angle BNA=45^{\circ}
и KN=AB
(как гипотенузы равных прямоугольных треугольников KCN
и ACB
), четырёхугольник AKNB
— равнобедренная трапеция, а C
— точка пересечения её диагоналей. Точка M
пересечения средней линии OO'
этой трапеции с отрезком CD
есть середина высоты O_{A}O_{B}
. Прямая O_{A}O_{B}
проходит через точку D
, так как \angle ACM=45^{\circ}
или \angle ACM=135^{\circ}
.
В то же время, OM\perp O_{A}O_{B}
, поэтому OM
— высота, а значит, и медиана равнобедренного треугольника COD
. Следовательно, M
— середина CD
, т. е. DM=\frac{1}{2}DC
.
Таким образом, точка M
получена из точки C
гомотетией с центром D
и коэффициентом \frac{1}{2}
. Следовательно, искомое ГМТ есть полуокружность, полученная из \Gamma
(без точек A
и B
) этой гомотетией.
Если же точка C
совпадает с D
, то и точка M
совпадает с D
.
Второй способ. Пусть O_{A}
и O_{B}
— центры квадратов, построенных на катетах AC
и BC
соответственно, O
— середина AB
, M
— середина отрезка O_{A}O_{B}
, P
и Q
— середины катетов соответственно AC
и BC
(рис. 2). Тогда
\overrightarrow{OO_{A}}=\overrightarrow{OP}+\overrightarrow{PO_{A}}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OC})+\overrightarrow{PO_{A}},
\overrightarrow{OO_{B}}=\overrightarrow{OQ}+\overrightarrow{QO_{B}}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})+\overrightarrow{QO_{B}},
\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OO_{A}}+\overrightarrow{OO_{B}})=\frac{1}{4}(\overrightarrow{OA}+\overrightarrow{OC}+2\overrightarrow{PO_{A}}+\overrightarrow{OB}+\overrightarrow{OC}+2\overrightarrow{QO_{B}})=
=\frac{1}{4}(2\overrightarrow{OC}+2\overrightarrow{PO_{A}}+2\overrightarrow{QO_{B}})=\frac{1}{2}(\overrightarrow{OC}+\overrightarrow{PO_{A}}+\overrightarrow{QO_{B}})=
=\frac{1}{2}\overrightarrow{OC}+\frac{1}{2}(\overrightarrow{PO_{A}}+\overrightarrow{QO_{B}}).
При повороте на 90^{\circ}
относительно произвольной точки, вектор \overrightarrow{PC}
переходит в вектор, равный \overrightarrow{PO_{A}}
, а вектор \overrightarrow{QB}
переходит в вектор, равный \overrightarrow{QO_{B}}
. Значит, при этом повороте вектор \overrightarrow{PC}+\overrightarrow{QB}
, равный вектору
\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\overrightarrow{AB}=\overrightarrow{OB},
переходит в вектор, равный вектору \overrightarrow{PO_{A}}+\overrightarrow{QO_{B}}
.
Таким образом,
\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OC}+\overrightarrow{a},
где \overrightarrow{a}
— вектор, полученный из вектора \frac{1}{2}\overrightarrow{OB}
при повороте на 90^{\circ}
.
Значит, точка M
получена из точки C
в результате композиции гомотетии с центром O
и коэффициентом \frac{1}{2}
и параллельного переноса на фиксированный вектор \overrightarrow{a}
.
Следовательно, если D
— середина данной полуокружности, то искомое ГМТ есть полуокружность, центр которой — середина OD
, радиус — половина радиуса данной полуокружности, а диаметр параллелен AB
(рис. 2).
Автор: Табов Й. (Болгария)
Источник: Турнир городов. — 1989-1990, XII, осенний тур, младшие классы, основной вариант

