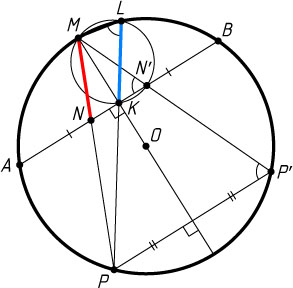
4330. Неравенство Эрдёша. Точка P
, лежащая на большей из двух дуг AB
окружности, соединена с серединой M
меньшей дуги AB
. Хорды PL
и PM
пересекают хорду AB
соответственно в её середине K
и в некоторой точке N
. Сравните отрезки KL
и MN
.
Ответ. KL\lt MN
.
Указание. Рассмотрите симметрию относительно прямой MK
. Далее примените метод вспомогательной окружности. (Или примените теорему синусов к треугольнику KLM
.)
Решение. Первый способ. Прямая KM
проходит через середины дуги AB
и середину хорды AB
, поэтому прямая MK
содержит диаметр окружности. Значит, окружность симметрична относительно этой прямой.
Предположим, что точка P
отлична от середины большей дуги AB
(иначе KL=MN
). Пусть P'
— точка, симметричная точке P
относительно прямой MK
. Тогда P'
лежит на окружности, PP'\parallel AB
, а точка N'
пересечения отрезков AB
и MP'
симметрична точке N
относительно MK
. Поэтому MN=MN'
.
Из теоремы о вписанных углах следует, что
\angle KN'M=\angle PP'M=\angle PLM.
Значит, из точек N'
и L
отрезок MK
виден под одним и тем же углом, причём эти точки лежат по одну сторону от MK
. Поэтому, точки K
, M
, L
и N'
лежат на одной окружности, а так как MK\perp AB
, то MN'
— диаметр этой окружности. Следовательно,
MN=MN'\gt KL
(диаметр есть наибольшая хорда окружности).
Второй способ. Пусть MT
— диаметр окружности. Обозначим \angle PMT=\alpha
и \angle LMT=\beta
. Тогда Поскольку \angle TPM=\angle MKN=90^{\circ}
, то
\angle MLP=\angle MTP=90^{\circ}-\alpha.
Значит, KM=MN\cos\alpha
.
По теореме синусов из треугольника KLM
получаем
\frac{KL}{\sin\beta}=\frac{KM}{\sin(90^{\circ}-\alpha)}=\frac{KM}{\cos\alpha}=MN.
Следовательно,
KL=MN\cos\beta\lt MN.
Источник: Хонсбергер Р. Математические изюминки. — М.: Наука, 1992. — Задача 38, с. 70
Источник: Журнал «Mathematics Magazine». — 1976, том 49, № 4, задача 949, с. 217
Источник: Венгерские математические олимпиады. — 2005-2006
Источник: Журнал «Crux Mathematicorum». — 2010, № 5, задача 5, с. 284
