4335. Угол при вершине A
равнобедренного треугольника ABC
(AB=AC
) равен 20^{\circ}
. На стороне AB
отложим отрезок AD
, равный BC
. Найдите угол BCD
.
Ответ. 70^{\circ}
.
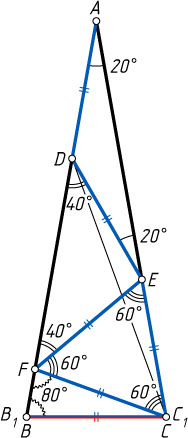
Решение. Первый способ. Будем поочерёдно строить на сторонах AC
и AB
(или, может быть, на их продолжениях) точки E
, F
, C_{1}
и B_{1}
(рис. 1) так, что
AD=DE=EF=FC_{1}=C_{1}B_{1}.
Последовательные вычисления углов треугольников ADE
, DEF
, EFC_{1}
, FC_{1}B_{1}
показывают, что
\angle AC_{1}B_{1}=\angle AB_{1}C_{1}=80^{\circ},
поэтому точка B_{1}
совпадает с точкой B
, а точка C_{1}
— с точкой C
. Кроме того, все углы треугольника EFC
равны 60^{\circ}
, а значит, DE=EF=EC
. Следовательно,
\angle DCE=\frac{1}{2}(180^{\circ}-\angle DEC)=10^{\circ}~\mbox{и}
\angle BCD=\angle BCA-\angle DCA=80^{\circ}-10^{\circ}=70^{\circ}.
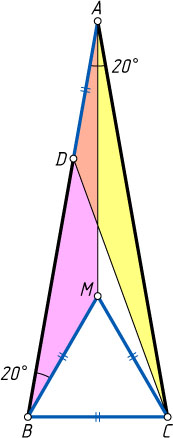
Второй способ. На высоте AH
данного треугольника отметим такую точку M
, что треугольник BMC
— равносторонний (рис. 2). Поскольку
AB=AC,~BM=BC=AD,
\angle ABM=\angle ABC-\angle MBC=80^{\circ}-60^{\circ}=20^{\circ}=\angle DAC,
то треугольники ABM
и CAD
равны по двум сторонам и углу между ними. Поэтому \angle ACD=\angle BAM=10^{\circ}
. Следовательно,
\angle BCD=\angle BCA-\angle ACD=80^{\circ}-10^{\circ}=70^{\circ}.
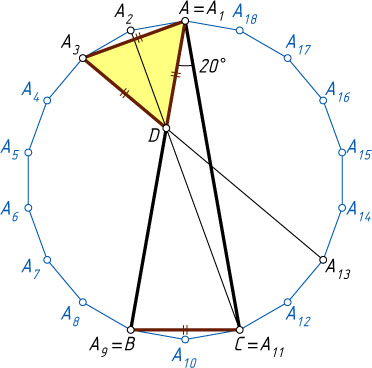
Третий способ. Рассмотрим правильный восемнадцатиугольник A_{1}\dots A_{18}
(рис. 3) Градусные меры дуг его описанной окружности, заключённых между соседними вершинами, равны \frac{360^{\circ}}{18}=20^{\circ}
. Поэтому
\angle A_{9}A_{1}A_{11}=20^{\circ},~\angle A_{1}A_{9}A_{11}=\angle A_{1}A_{11}A_{9}=80^{\circ},
Если считать, что A=A_{1}
, B=A_{9}
, C=A_{11}
, то точка пересечения диаметра A_{2}A_{11}
и симметричных ему хорд A_{3}A_{13}
и A_{1}A_{9}
— это точка D
. Действительно, треугольник A_{1}A_{3}D
равносторонний, так как
\angle DAA_{3}=\angle BAA_{3}=60^{\circ},~\angle AA_{3}D=\angle AA_{3}A_{13}=60^{\circ},
поэтому AD=A_{1}D=A_{1}A_{3}=A_{9}A_{11}=BC
. Следовательно,
\angle BCD=\angle BCA_{2}=70^{\circ}.
Примечание. См. также статью М.Васильева и Т.Корчёмкиной «Вспомогательные равносторонние треугольники», Квант, 2023, N3, с.37-42.
Автор: Шарыгин И. Ф.
Источник: Журнал «Crux Mathematicorum». — 1977, № 2, задача 175 (1976, 171), с. 49
Источник: Турнир городов. — 1991-1992, XIII, осенний тур, младшие классы, основной вариант
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 932, с. 114
Источник: Журнал «Квант». — 2023, № 3, с. 39, задача 4 (фрагмент)


