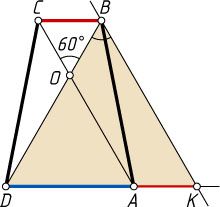
4337. В трапеции ABCD
(AD
— основание) диагональ AC
равна сумме оснований, а угол между диагоналями равен 60^{\circ}
. Докажите, что трапеция равнобедренная.
Указание. Перенесите диагональ AC
на вектор \overrightarrow{CB}
.
Решение. Первый способ. Пусть AC=AD+BC
, а диагонали трапеции пересекаются в точке O
. Через вершину B
проведём прямую, параллельную диагонали AC
. Пусть K
— точка пересечения этой прямой с прямой AD
. Тогда AKBC
— параллелограмм, поэтому \angle KBD=\angle AOD
и
AK=BC,~KB=AC=BC+AD=AK+AD=KD.
Значит, треугольник KBD
— равнобедренный (KB=KD
). Поскольку углы при основании равнобедренного треугольника — острые, то угол KBD
не может быть равен 120^{\circ}
. Следовательно, он равен 60^{\circ}
. Тогда треугольник KBD
— равносторонний. Поэтому KB=BD=AC
, т. е. диагонали трапеции равны между собой. Значит, она равнобедренная.
Второй способ. Пусть AB=a
и CD=b
— основания трапеции, AC=a+b
— диагональ, O
— точка пересечения диагоналей. Из подобия треугольников COD
и AOB
получаем
\frac{OC}{OA}=\frac{b}{a}~\Rightarrow~\frac{OC}{a+b}=\frac{b}{a+b}~\Rightarrow~OC=b,
поэтому треугольник COD
равнобедренный с основанием OD
, а так как угол при основании равнобедренного треугольника не может быть тупым, то \angle COD=\angle CDO=60^{\circ}
. Значит, треугольник COD
равносторонний. Тогда и треугольник AOB
равносторонний, поэтому BD=a+b=AC
. Диагонали трапеции ABCD
равны, следовательно, она равнобедренная (см. задачу 1915).
Автор: Смирнов С. К.
Источник: Турнир городов. — 1991-1992, XIII, весенний тур, младшие классы, тренировочный вариант
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1992, 8 кл.
Источник: Новосибирская устная олимпиада по геометрии. — 2023, задача 4, 9 класс
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 92.16
