4339. На каждой стороне параллелограмма выбрано по точке (выбранные точки отличны от вершин параллелограмма). Точки, лежащие на соседних (имеющих общую вершину) сторонах, соединены отрезками. Докажите, что центры описанных окружностей четырёх получившихся треугольников — вершины параллелограмма.
Указание. Примените параллельный перенос.
Решение. Пусть точки M
, N
, P
и Q
лежат на сторонах соответственно AB
, BC
, CD
и AD
параллелограмма ABCD
.
Введём обозначения: l_{XY}
— серединный перпендикуляр к отрезку XY
, O_{\triangle FGH}
— центр окружности, описанной около треугольника FGH
.
Пусть L
— точка пересечения прямых l_{AQ}
и l_{MB}
, T
— точка пересечения прямых l_{DQ}
и l_{CP}
. При параллельном переносе на вектор \overrightarrow{LT}
прямая l_{AQ}
переходит в параллельную ей прямую, проходящую через точку T
, т. е. в прямую l_{DQ}
, а прямая l_{MB}
— в прямую l_{CP}
.
Заметим, что расстояние между параллельными прямыми l_{AM}
и l_{BM}
равно расстоянию между прямыми l_{CP}
и l_{DP}
, так как каждое из этих расстояний равно половине стороны AB
параллелограмма ABCD
. Значит, при рассматриваемом параллельном переносе прямая l_{AM}
переходит в прямую l_{PD}
.
Поскольку расстояние между параллельными прямыми l_{AQ}
и l_{DQ}
равно расстоянию между прямыми l_{BN}
и l_{CN}
(каждое из этих расстояний равно половине стороны BC
параллелограмма ABCD
), то при рассматриваемом параллельном переносе прямая l_{BN}
переходит в прямую l_{CN}
.
Из доказанного следует, что параллелограмм, образованный пересечением прямых l_{AM}
, l_{BM}
, l_{AQ}
и l_{BN}
переходит в параллелограмм, образованный пересечением прямых l_{DP}
, l_{CP}
, l_{DQ}
и l_{CN}
. Поэтому диагональ O_{\triangle AMQ}O_{\triangle MBN}
первого из этих параллелограммов переходит в соответствующую диагональ O_{\triangle QPD}O_{\triangle NCP}
второго. Следовательно, четырёхугольник O_{\triangle AMQ}O_{\triangle MBN}O_{\triangle NCP}O_{\triangle QPD}
— параллелограмм.
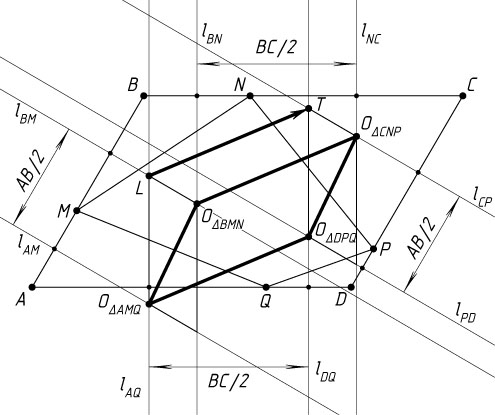
Автор: Куланин Е. Д.
Источник: Турнир городов. — 1992-1993, XIV, осенний тур, младшие классы, тренировочный вариант
