4341. Биссектриса угла A
треугольника ABC
пересекает описанную окружность в точке D
. Пусть P
— точка, симметричная центру вписанной окружности треугольника ABC
относительно середины стороны BC
, M
— вторая точка пересечения прямой DP
с описанной окружностью. Докажите, что расстояние от точки M
до одной из вершин A
, B
, C
равно сумме расстояний от M
до двух других вершин.
Решение. Обозначим через I
центр вписанной окружности треугольника ABC
. Пусть \angle BAC=2\alpha
, \angle ABC=2\beta
.
Поскольку BID
— внешний угол треугольника AIB
, то
\angle BID=\angle BAI+\angle ABI=\alpha+\beta.
С другой стороны, из теоремы о вписанных углах следует, что
\angle IBD=\angle IBC+\angle CBD=\angle IBC+\angle CAD=\beta+\alpha.
Значит, \angle BID=\angle DBI
. Поэтому треугольник BID
— равнобедренный. Следовательно, DB=DI
. Аналогично докажем, что DI=DC
.
Обозначим DB=DI=DC=r
. Пусть R
— радиус описанной окружности треугольника ABC
.
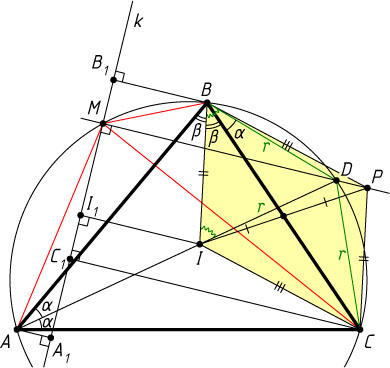
Через точку M
проведём прямую k
, перпендикулярную DM
. Пусть I_{1}
, A_{1}
, B_{1}
и C_{1}
— проекции точек I
, A
, B
и C
на эту прямую. Тогда
MA=2R\sin\angle MDA=2R\sin\angle MDI=2R\cdot\frac{MI_{1}}{DI}=2R\cdot\frac{MI_{1}}{r},
MB=2R\sin\angle MDB=2R\cdot\frac{MB_{1}}{DB}=2R\cdot\frac{MB_{1}}{r},
MC=2R\sin\angle MDC=2R\cdot\frac{MC_{1}}{DC}=2R\cdot\frac{MC_{1}}{r},
Поскольку точка P
симметрична точке I
относительно середины стороны BC
, то BICP
— параллелограмм. Отрезки MB_{1}
, MI_{1}
и MC_{1}
— проекции соответственно стороны BP
, диагонали IP
и стороны CP
этого параллелограмма на прямую k
. Одна из этих проекций равна сумме двух других (на нашем рисунке MC_{1}=MI_{1}+C_{1}I_{1}=MI_{1}+MB_{1}=B_{1}I_{1}
).
Следовательно, один из трёх отрезков MA
, MB
и MC
равен сумме двух других. На нашем рисунке
MA+MB=2R\cdot\frac{MI_{1}}{r}+2R\cdot\frac{MB_{1}}{r}=
=\frac{2R}{r}(MI_{1}+MB_{1})=\frac{2R}{r}(MI_{1}+I_{1}C_{1})=\frac{2R}{r}\cdot MC_{1}=MC.
Автор: Гордон В.
Источник: Турнир городов. — 1992-1993, XIV, осенний тур, старшие классы, основной вариант
