4350. Дан равносторонний треугольник ABC
. Для произвольной точки P
внутри треугольника рассмотрим точки A'
и C'
пересечения прямых AP
с BC
и CP
с AB
. Найдите геометрическое место точек P
, для которых отрезки AA'
и CC'
равны.
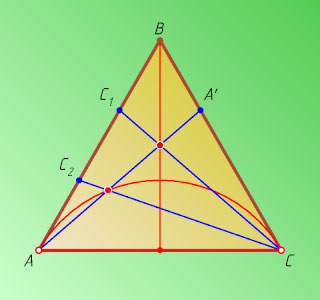
Ответ. Фигура состоящая из стороны AC
(без точек A
и C
), проведённой к ней высоты BH
и лежащей внутри треугольника ABC
дуги окружности, из каждой точки которой отрезок AC
виден под углом 120^{\circ}
(рис. 1).
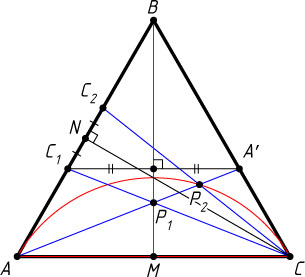
Решение. Выберем произвольную точку A'
на стороне BC
и проведём отрезок AA'
(рис. 2). Докажем, что среди отрезков с началом в точке C
и концом на стороне AB
имеются только два, равных отрезку AA'
. Это такие отрезки CC_{1}
и CC_{2}
, что
\angle C_{1}CA=\angle A'AC,~\angle C_{2}CB=\angle A'AC.
Действительно, при симметрии треугольника относительно высоты, проведённой из вершины B
, отрезок CC_{1}
переходит в отрезок AA'
, поэтому CC_{1}=AA'
. При симметрии относительно высоты, проведённой из вершины C
, отрезок CC_{2}
переходит в отрезок CC_{1}
, поэтому CC_{2}=CC_{1}
.
То, что нет других таких точек C'
, что CC'=AA'
следует из того, что из данной точки к данной прямой можно провести не более двух наклонных данной длины.
Рассмотрим точки P_{1}
и P_{2}
пересечения AA'
с прямыми CC_{1}
и CC_{2}
соответственно. Точка P_{1}
лежит на высоте треугольника ABC
, проведённой из вершины B
, а для точки P_{2}
имеем:
\angle AP_{2}C=180^{\circ}-\angle A'AC-\angle C_{2}CA=180^{\circ}-\angle A'AC-(60^{\circ}-\angle A'AC)=120^{\circ},
т. е. отрезок AC
виден из точки P_{2}
под углом 120^{\circ}
. Значит, геометрическое место точек P_{2}
— это дуга окружности (без концов A
и C
). Ясно, что на этой дуге лежит центр треугольника ABC
.
Проводя приведённые рассуждения в обратном порядке, убедимся, что все точки этой дуги удовлетворяют условию задачи.
Источник: Московская математическая олимпиада. — 1995, LVIII, 9 класс
Источник: Турнир городов. — 1994-1995, XVI, весенний тур, младшие классы, основной вариант
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 2, с. 27

