4365. Отрезок AB
пересекает две равные окружности и параллелен их линии центров, причём все точки пересечения прямой AB
с окружностями лежат между A
и B
. Через точку A
проводятся касательные к окружности, ближайшей к A
, через точку B
— касательные к окружности, ближайшей к B
. Оказалось, что эти четыре касательные образуют четырёхугольник, содержащий внутри себя обе окружности. Докажите, что в этот четырёхугольник можно вписать окружность.
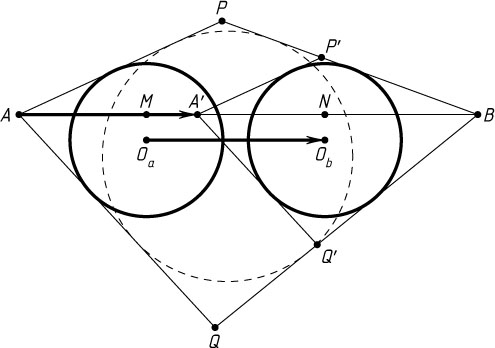
Решение. Обозначим через O_{A}
и O_{B}
центры окружностей, ближайших соответственно к A
и B
, P
и Q
— вершины четырёхугольника APBQ
, о котором говорится в условии задачи. Пусть \mathbf{T}
— параллельный перенос на вектор \overrightarrow{O_{A}O_{B}}
, \mathbf{H}
— гомотетия с центром B
и коэффициентом \frac{AB}{AB-O_{A}O_{B}}
.
Параллельный перенос \mathbf{T}
переводит окружность с центром O_{A}
и касательные к ней AP
и AQ
в окружность с центром O_{B}
и касательные к ней A'P'
и A'Q'
соответственно. При этом A'P'\parallel AP
, A'Q'\parallel AQ
и четырёхугольник A'P'BQ'
описанный.
Докажем, что A'B=AB-O_{A}O_{B}
. Действительно, если M
и N
— середины хорд, высекаемых прямой AB
из окружностей с центрами O_{A}
и O_{B}
соответственно, то AM=A'N
. Поэтому
A'B=A'N+NB=AM+NB=AB-MN=AB-O_{A}O_{B}.
Значит,
\frac{AB}{A'B}=\frac{AB}{AB-O_{A}O_{B}}.
Гомотетия \mathbf{H}
переводит точку A'
в точку A
, отрезок A'P'
— в отрезок AP
, A'Q'
— в AQ
. Поэтому четырёхугольник A'P'BQ'
переходит в четырёхугольник APBQ
. Следовательно, четырёхугольник APBQ
также описанный.
Автор: Кожевников П. А.
Источник: Турнир городов. — 1998-1999, XX, осенний тур, младшие классы, основной вариант
