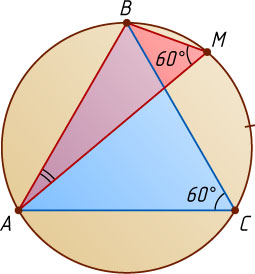
4371. Окружность описана около равностороннего треугольника ABC
. На дуге BC
, не содержащей точку A
, расположена точка M
, делящая градусную меру этой дуги в отношении 1:2
. Найдите углы треугольника AMB
.
Ответ. 20^{\circ}
, 60^{\circ}
, 100^{\circ}
или 40^{\circ}
, 60^{\circ}
, 80^{\circ}
.
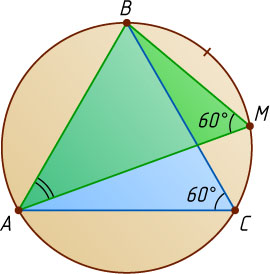
Решение. Пусть \smile BM:\smile CM=1:2
. Тогда
\smile BM=\frac{1}{3}\smile BMC=\frac{1}{3}\cdot120^{\circ}=40^{\circ}.
По теореме о вписанном угле
\angle BAM=\frac{1}{2}\smile BM=20^{\circ},
а так как вписанные углы AMB
и ACB
опираются на одну и ту же дугу, то \angle AMB=\angle ACB=60^{\circ}
. Следовательно,
\angle ABM=180^{\circ}-20^{\circ}-60^{\circ}=100^{\circ}.
Если же \smile BM:\smile CM=2:1
, то аналогично найдём, что
\angle BAM=40^{\circ},~\angle AMB=60^{\circ},~\angle ABM=80^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.4, с. 103

