4372. Точки A
, B
, C
и D
последовательно расположены на окружности. Известно, что градусные меры меньших дуг AB
, BC
, CD
и AD
относятся как 1:3:5:6
. Найдите углы четырёхугольника ABCD
.
Ответ. 96^{\circ}
, 132^{\circ}
, 84^{\circ}
, 48^{\circ}
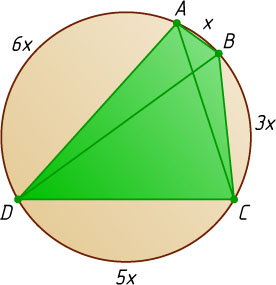
Решение. Пусть градусная мера меньшей дуги AB
равна x
. Тогда градусные меры последовательных дуг BC
, CD
и AD
соответственно равны 3x
, 5x
и 6x
. Из уравнения x+3x+5x+6x=360^{\circ}
находим, что x=24^{\circ}
, следовательно, градусные меры последовательных дуг AB
, BC
, CD
и AD
соответственно равны 24^{\circ}
, 3\cdot24^{\circ}=72^{\circ}
, 5\cdot24^{\circ}=120^{\circ}
и 6\cdot24^{\circ}=144^{\circ}
.
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается, следовательно,
\angle BAD=\frac{1}{2}\smile BCD=\frac{1}{2}(72^{\circ}+120^{\circ})=96^{\circ},~\angle ABC=\frac{1}{2}\smile ADC=\frac{1}{2}(144^{\circ}+120^{\circ})=132^{\circ},
\angle BCD=\frac{1}{2}\smile BAD=\frac{1}{2}(24^{\circ}+144^{\circ})=84^{\circ},~\angle ADC=\frac{1}{2}\smile ABC=\frac{1}{2}(24^{\circ}+72^{\circ})=48^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.5, с. 103
