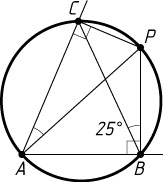
4373. Из точки P
, расположенной внутри острого угла с вершиной A
, опущены перпендикуляры PB
и PC
на стороны угла. Известно, что \angle CBP=25^{\circ}
. Найдите угол CAP
.
Ответ. 25^{\circ}
.
Решение. Из точек B
и C
отрезок AP
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AP
. Вписанные в эту окружность углы CAP
и CBP
опираются на одну и ту же дугу, следовательно,
\angle CAP=\angle CBP=25^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.7, с. 103
