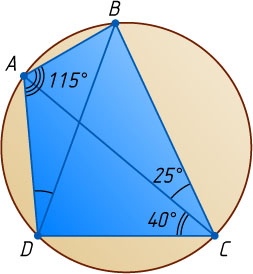
4375. В выпуклом четырёхугольнике ABCD
известно, что \angle ACB=25^{\circ}
, \angle ACD=40^{\circ}
и \angle BAD=115^{\circ}
. Найдите угол ADB
.
Ответ. 25^{\circ}
.
Решение. Четырёхугольник ABCD
— выпуклый, поэтому луч CA
проходит между сторонами угла BCD
, значит,
\angle BCD=\angle ACB+\angle ACD=25^{\circ}+40^{\circ}=65^{\circ}.
Тогда
\angle BCD+\angle BAD=65^{\circ}+115^{\circ}=180^{\circ},
поэтому четырёхугольник ABCD
— вписанный, т. е. точки A
, B
, C
и D
лежат на одной окружности. Вписанные в эту окружность углы ADB
и ACB
опираются на одну и ту же дугу, следовательно,
\angle ADB=\angle ACB=25^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.10, с. 103
