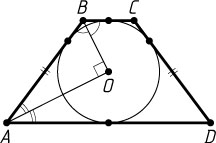
4383. Окружность радиуса 2 вписана в равнобочную трапецию. Точка касания делит боковую сторону трапеции в отношении 1:4
. Найдите площадь трапеции.
Ответ. 20.
Решение. Пусть окружность радиуса 2 с центром в точке O
касается боковой стороны AB
равнобочной трапеции ABCD
в точке M
, причём \frac{BM}{AM}=\frac{1}{4}
.
Центр окружности, вписанной в угол, расположен на его биссектрисе, поэтому AO
и BO
— биссектрисы углов BAD
и ABC
, а так как сумма этих углов равна 180^{\circ}
, то
\angle AOB=180^{\circ}-(\angle OAB+\angle OBA)=180^{\circ}-90^{\circ}=90^{\circ}.
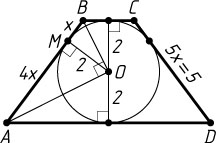
Положим BM=x
, AM=4x
. Отрезок OM
— высота прямоугольного треугольника, проведённая из вершины прямого угла, поэтому OM^{2}=AM\cdot BM
, или 4=4x^{2}
, откуда находим, что x=1
. Значит, AB=5x=5
.
Суммы противоположных сторон описанного четырёхугольника равны между собой, поэтому
AD+BC=AB+CD=2AB=10,
а так как высота трапеции равна диаметру вписанной окружности, т. е. 4, то
S_{ABCD}=\frac{AD+BC}{2}\cdot4=5\cdot4=20.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 2009 июль, устный экзамен
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.39, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.39.1, с. 38

