4418. Биссектриса CD
угла ACB
при основании BC
равнобедренного треугольника ABC
делит сторону AB
так, что AD=BC
. Найдите биссектрису CD
и площадь треугольника ABC
, если BC=2
.
Ответ. 2; \tg72^{\circ}=\sqrt{5+2\sqrt{5}}
.
Указание. Докажите, что квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой.
Решение. Первый способ. Докажем сначала, что квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой.
Пусть M
— точка пересечения продолжения биссектрисы CD
треугольника ABC
с описанной около этого треугольника окружностью. Тогда треугольник CBD
подобен треугольнику CMA
по двум углам. Поэтому
\frac{CD}{AC}=\frac{BC}{CM},~\mbox{или}~CD(CD+DM)=AC\cdot BC,
CD^{2}+CD\cdot DM=AC\cdot BC.
Следовательно,
CD^{2}=AC\cdot BC-CD\cdot DM=AC\cdot BC-AD\cdot BD
(CD\cdot DM=AD\cdot DB
по теореме о произведениях отрезков пересекающихся хорд).
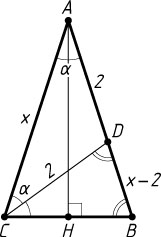
Вернёмся к нашей задаче. Обозначим AB=AC=x
. Тогда BD=2-x
и из доказанного утверждения следует, что
CD^{2}=AC\cdot BC-AD\cdot BD=x\cdot2-2\cdot(x-2)=2x-2x+4=4.
Значит, CD=2
.
Поскольку CD=AD=BC
, треугольники ACD
и CBD
— равнобедренные. Пусть \angle BAC=\alpha
. Тогда
\angle ACD=\angle CAD=\alpha,~\angle CBD=\angle BDC=\angle CAD+\angle ACD=2\alpha,
а так как сумма углов треугольника BCD
равна 180^{\circ}
, получаем уравнение
\alpha+2\alpha+2\alpha=180^{\circ},
из которого находим, что \alpha=36^{\circ}
.
Пусть AH
— высота треугольника ABC
. Тогда BH=CH=1
. Из прямоугольного треугольника ABH
находим, что
AH=BH\tg\angle CBA=1\cdot\tg2\alpha=\tg72^{\circ}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot2\tg72^{\circ}=\tg72^{\circ}.
Если воспользоваться свойством биссектрисы треугольника, то можно легко вычислить \tg72^{\circ}
. Действительно,
\frac{AC}{BC}=\frac{AD}{BD}~\Rightarrow~\frac{x}{2}=\frac{2}{x-2}~\Rightarrow~x^{2}-2x-4=0~\Rightarrow~x=1+\sqrt{5}~\Rightarrow
\Rightarrow~\cos72^{\circ}=\cos\angle ABC=\frac{BH}{AB}=\frac{1}{1+\sqrt{5}}~\Rightarrow
\Rightarrow~\tg72^{\circ}=\sqrt{\frac{1}{\cos^{2}72^{\circ}}-1}=\sqrt{(1+\sqrt{5})^{2}-1}=\sqrt{5+2\sqrt{5}}.
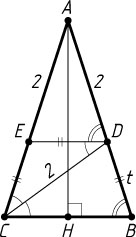
Второй способ. Пусть прямая, проведённая через точку D
параллельно BC
, пересекает сторону AC
в точке E
. Тогда \angle CDE=\angle BCD=\angle DCE
, поэтому треугольник CDE
— равнобедренный, значит, BD=CE=DE
, а так как \angle ADE=\angle ABC
и AD=BC
, то треугольник BCD
равен треугольнику ADE
по двум сторонам и углу между ними. Следовательно, CD=AE=AD=2
.
Обозначим CE=BD=t
. По свойству биссектрисы треугольника \frac{AD}{AC}=\frac{BD}{BC}
, или \frac{2}{t+2}=\frac{t}{2}
, откуда t=\sqrt{5}-1
, поэтому AB=t+2=\sqrt{5}+1
.
Пусть AH
— высота треугольника ABC
. По теореме Пифагора
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{(\sqrt{5}+1)^{2}-1}=\sqrt{5+2\sqrt{5}}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot2\cdot\sqrt{5+2\sqrt{5}}=\sqrt{5+2\sqrt{5}}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 2005 вариант 1, № 6
Источник: Вступительные экзамены и олимпиады по математике 2003—2005 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2006. — с. 209
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.24, с. 41

