4431. На данной окружности зафиксированы две точки A
и B
, а точка M
пробегает всю окружность. Из середины K
отрезка MB
опускается перпендикуляр на прямую MA
. Основание этого перпендикуляра обозначается через P
. Найдите геометрическое место точек P
.
Ответ. Окружность без двух точек.
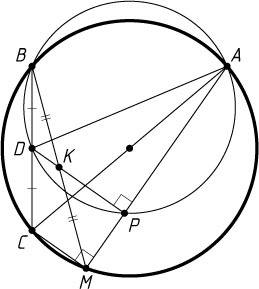
Решение. Пусть C
— точка, диаметрально противоположная точке A
, D
— середина отрезка BC
. Тогда KD
— средняя линия треугольника CMB
, поэтому KD\parallel MC
. С другой стороны, точка M
лежит на окружности с диаметром AC
, значит, CM\perp AM
. В то же время, KP\perp AM
по условию. Поэтому KP\parallel MC
. Следовательно, точки P
, K
и D
лежат на одной прямой. Поскольку \angle APD=90^{\circ}
, точка P
лежит на окружности с диаметром AD
.
Докажем, что любая точка этой окружности, кроме A
и B
, удовлетворяет условию задачи, т. е. для каждой отличной от A
и B
точки P
окружности с диаметром AD
на данной окружности найдётся такая точка M
, для которой перпендикуляр, восставленный к хорде AM
в точке P
, проходит через середину K
хорды MB
.
Действительно, пусть прямая AP
второй раз пересекает исходную окружность в точке M
. Если AC
— диаметр этой окружности, то CM\perp AM
, а так как точка P
лежит на окружности с диаметром AD
, то PD\perp AM
. Значит, PD\parallel MC
. В то же время, если K
— середина MB
, то KD
— средняя линия треугольника MBC
, значит, KD\parallel MC
. Следовательно, точка K
лежит на прямой PD
, т. е. P
— основание перпендикуляра, опущенного из середины хорды MB
на MA
, что и требовалось доказать.
