4454. На сторонах AB
и BC
треугольника ABC
выбраны точки K
и L
соответственно, причём \angle KCB=\angle LAB=\alpha
. Из точки B
опущены перпендикуляры BD
и BE
на прямые AL
и CK
соответственно. Точка F
— середина стороны AC
. Найдите углы треугольника DEF
.
Решение. Пусть M
и N
— середины сторон AB
и BC
соответственно. Обозначим \angle ABC=\beta
. Тогда
\angle AMF=\angle CNF=\angle ABC=\beta.
Поскольку EN
и DM
медианы прямоугольных треугольников CBE
и ADB
, проведённые из вершин прямых углов, то
EN=\frac{1}{2}BC=NC=MF,~DM=\frac{1}{2}AB=AM=NF.
Кроме того, по теореме о внешнем угле треугольника
\angle BNE=2\alpha=\angle BMD,
значит,
\angle ENF=180^{\circ}-\angle BNE-\angle CNF=180^{\circ}-2\alpha-\beta,
\angle DMF=180^{\circ}-\angle BMD-\angle AMF=180^{\circ}-2\alpha-\beta.
Поэтому треугольники ENF
и DMF
равны по двум сторонам и углу между ними. Следовательно, EF=DF
.
Поскольку \angle MFD=\angle FEN
и \angle NFE=\angle MDF
(из равенства треугольников ENF
и DMF
), то
\angle MFD+\angle NFE=\angle MFD+\angle MDF=180^{\circ}-\angle DMF=2\alpha+\beta.
С другой стороны
\angle MFD+\angle NFE=\angle MFN+\angle DFE=\beta+\angle DFE.
Из равенства
2\alpha+\beta=\beta+\angle DFE
находим, что \angle DFE=2\alpha
. Тогда
\angle DEF=\angle EDF=90^{\circ}-\alpha.
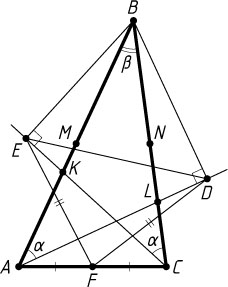
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1995 г., второй тур, 10 класс
Источник: Берлов С. Л., Иванов С. В., Кохась К. П. Петербургские математические олимпиады. — СПб.—М.—Краснодар: Лань, 2003. — с. 48
