4455. Вокруг остроугольного треугольника ABC
описана окружность. Продолжения высот треугольника, проведённых из вершин A
и C
, пересекают окружность в точках E
и F
соответственно, D
— произвольная точка на (меньшей) дуге AC
, K
— точка пересечения DF
и AB
, L
— точка пересечения DE
и BC
. Докажите, что прямая KL
проходит через ортоцентр треугольника ABC
.
Указание. Точка, симметричная ортоцентру треугольника относительно стороны треугольника, лежит на описанной окружности.
Решение. Пусть H
— ортоцентр треугольника ABC
. Известно, что точка, симметричная ортоцентру треугольника относительно стороны треугольника, лежит на описанной окружности, поэтому
\angle HEL=\angle EHL,~\angle AHK=\angle AFK.
Вписанные углы AED
и AFD
опираются на одну и ту же дугу, значит,
\angle EHL=\angle HEL=\angle AED=\angle AFD=\angle AFK=\angle AHK.
Следовательно, точки K
, H
и L
лежат на одной прямой, что и требовалось доказать.
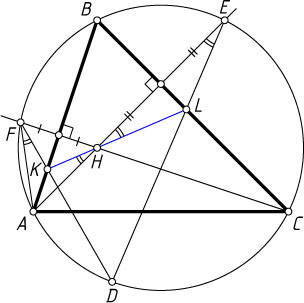
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1995 г., второй тур, 11 класс
Источник: Берлов С. Л., Иванов С. В., Кохась К. П. Петербургские математические олимпиады. — СПб.—М.—Краснодар: Лань, 2003. — с. 48
