4456. На плоскости даны две пересекающиеся окружности. Точка A
— одна из двух точек пересечения. В каждой окружности проведён диаметр, параллельный касательной в точке A
к другой окружности, причём эти диаметры не пересекаются. Докажите, что концы этих диаметров лежат на одной окружности.
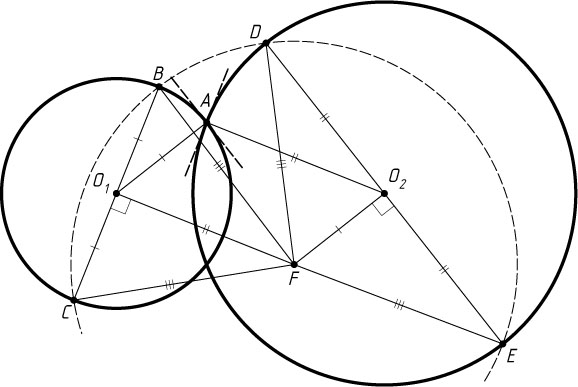
Решение. Пусть BC
— диаметр окружности с центром O_{1}
, параллельный касательной в точке A
к окружности с центром O_{2}
, DE
— соответствующий диаметр окружности с центром O_{2}
. Докажем, что точка F
пересечения серединных перпендикуляров к отрезкам BC
и DE
— центр окружности, проходящей через точки B
, C
, D
и E
.
Действительно, четырёхугольник AO_{1}FO_{2}
— параллелограмм, так как прямые O_{1}A
и O_{2}F
перпендикулярны одной и той же прямой DE
(радиус O_{1}A
перпендикулярен касательной к окружности с центром O_{2}
, значит, он перпендикулярен и прямой DE
, параллельной этой касательной). Аналогично, прямые O_{2}A
и O_{1}F
перпендикулярны одной и той же прямой BC
.
Противоположные стороны параллелограмма попарно равны, поэтому
O_{2}F=O_{1}A=O_{1}B,~O_{1}F=O_{2}A=O_{2}D.
Значит, прямоугольные треугольники BO_{1}F
и DO_{2}F
равны по двум катетам. Следовательно, FB=FD
, а так как точка F
лежит на серединных перпендикулярах к отрезкам BC
и DE
, то
FC=FB=FD=FE.
Отсюда следует доказываемое утверждение.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1995 г., отборочный тур, 9 класс
Источник: Журнал «Квант». — 1995, № 5, с. 20, М1511; 1996, № 2, с. 14, М1511
Источник: Задачник «Кванта». — М1511
Источник: Берлов С. Л., Иванов С. В., Кохась К. П. Петербургские математические олимпиады. — СПб.—М.—Краснодар: Лань, 2003. — с. 51
