4519. Из медиан AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
составлен треугольник KMN
, а из медиан KK_{1}
, MM_{1}
и NN_{1}
треугольника KMN
— треугольник PQR
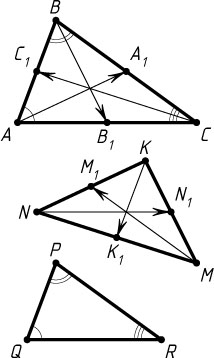
. Докажите, что третий треугольник подобен первому и найдите коэффициент подобия.
Ответ. \frac{3}{4}
.
Указание. \overrightarrow{PQ}=\overrightarrow{KK_{1}}=\frac{1}{2}(\overrightarrow{KN}+\overrightarrow{KM})
.
Решение. Пусть AA_{1}
, BB_{1}
, CC_{1}
— медианы треугольника ABC
, а KK_{1}
, MM_{1}
, NN_{1}
— медианы треугольника MNK
, причём
\overrightarrow{NK}=\overrightarrow{AA_{1}},~\overrightarrow{MN}=\overrightarrow{CC_{1}},~\overrightarrow{KM}=\overrightarrow{BB_{1}}.
Если PQR
— такой треугольник, что
\overrightarrow{PQ}=\overrightarrow{KK_{1}},~\overrightarrow{QR}=\overrightarrow{NN_{1}},~\overrightarrow{RP}=\overrightarrow{MM_{1}},
то
\overrightarrow{PQ}=\overrightarrow{KK_{1}}=\frac{1}{2}(\overrightarrow{KN}+\overrightarrow{KM})=\frac{1}{2}(\overrightarrow{BB_{1}}-\overrightarrow{AA_{1}})=
=\frac{1}{2}\left(\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})-\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AB})\right)=
=\frac{1}{4}(\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{BA})=\frac{1}{4}(\overrightarrow{BA}+\overrightarrow{BA}+\overrightarrow{BA})=
=\frac{1}{4}(3\overrightarrow{BA})=-\frac{3}{4}\overrightarrow{AB}.
Аналогично для векторов \overrightarrow{QR}
и \overrightarrow{RP}
.
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 28
