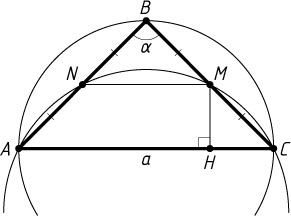
4548. В равнобедренном треугольнике ABC
параллельно основанию AC
проведена средняя линия MN
. Радиус окружности, описанной около трапеции ACMN
, в \frac{\sqrt{5}}{2}
раз больше радиуса окружности, описанной около треугольника ABC
. Найдите углы треугольника ABC
.
Ответ. \frac{\pi}{2}
, \frac{\pi}{4}
.
Решение. Обозначим AC=a
, \angle ABC=\alpha
, R
— радиус окружности, описанной около треугольника ABC
. По теореме синусов
R=\frac{a}{2\sin\alpha}=\frac{a}{4\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}}.
Пусть H
— проекция середины M
боковой стороны BC
на основание AC
. Тогда
HC=\frac{1}{2}(AC-MN)=\frac{1}{2}\left(a-\frac{a}{2}\right)=\frac{a}{4},~AH=a-\frac{a}{4}=\frac{3}{4}a.
Из прямоугольных треугольников CHM
и AHM
находим, что
MH=CH\tg\angle ACB=\frac{a}{4}\cdot\tg\left(\frac{\pi}{2}-\frac{\alpha}{2}\right)=\frac{a}{4}\ctg\alpha,
AM=\sqrt{AH^{2}+MH^{2}}=\sqrt{\frac{9}{16}a^{2}+\frac{a^{2}}{16}\ctg^{2}\frac{\alpha}{2}}=\frac{a}{4}\sqrt{9+\ctg^{2}\frac{\alpha}{2}}.
Пусть R_{1}
— радиус окружности, описанной около равнобедренной трапеции ACMN
. По теореме синусов
R_{1}=\frac{AM}{2\sin\angle ACM}=\frac{\frac{a}{4}\sqrt{9+\ctg^{2}\frac{\alpha}{2}}}{2\sin\left(\frac{\pi}{2}-\frac{\alpha}{2}\right)}=\frac{a\sqrt{9+\ctg^{2}\frac{\alpha}{2}}}{8\cos\frac{\alpha}{2}},
а так как R_{1}=\frac{\sqrt{5}}{2}R
, то
\frac{a\sqrt{9+\ctg^{2}\frac{\alpha}{2}}}{8\cos\frac{\alpha}{2}}=\frac{\sqrt{5}}{2}\cdot\frac{a}{4\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}},
откуда находим, что \sin^{2}\frac{\alpha}{2}=\frac{1}{2}
. Тогда
\cos\alpha=1-2\sin^{2}\frac{\alpha}{2}=1-2\cdot\frac{1}{2}=0.
Следовательно,
\angle ABC=\alpha=\frac{\pi}{2},~\angle BAC=\angle BCA=\frac{\pi}{4}.
Источник: Вступительный экзамен в МФТИ. — 1965, билет 6, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 65-6-4, с. 110
