4553. Около окружности описана равнобочная трапеция. Площадь четырёхугольника с вершинами в точках касания составляет \frac{3}{8}
площади трапеции. Найдите отношение оснований трапеции.
Ответ. 3.
Решение. Пусть вписанная окружность касается оснований AD=a
и BC=b
(a\gt b
) трапеции ABCD
в точках N
и L
соответственно, а боковых сторон AB
и CD
— соответственно в точках K
и M
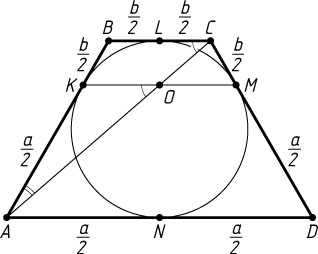
(рис. 1). Тогда
BK=BL=LC=CM,~AK=AN=ND=DM,
поэтому
\frac{AK}{AB}=\frac{AN}{AN+BL}=\frac{\frac{a}{2}}{\frac{a}{2}+\frac{b}{2}}=\frac{a}{a+b},~\frac{DM}{CD}=\frac{DN}{DN+CL}=\frac{\frac{a}{2}}{\frac{a}{2}+\frac{b}{2}}=\frac{a}{a+b},
значит, KM\parallel AD
. Если O
— точка пересечения AC
и KM
, то из подобия треугольников AKO
и ABC
находим, что
KO=BC\cdot\frac{AK}{AB}=b\cdot\frac{a}{a+b}=\frac{ab}{a+b}.
Аналогично, MO=b\cdot\frac{a}{a+b}
. Поэтому KM=KO+OM=\frac{2ab}{a+b}
.
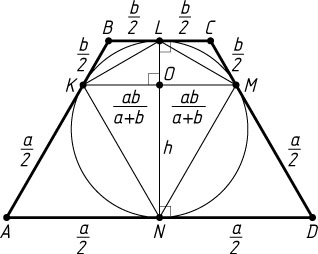
Пусть высота трапеции равна h
(рис. 2). Тогда
S_{ABCD}=\frac{1}{2}(AD+BC)h=\frac{1}{2}(a+b)h,
а так как NL\perp KM
, то
S_{KLMN}=\frac{1}{2}KM\cdot LN=\frac{1}{2}\cdot\frac{2ab}{a+b}\cdot h=\frac{abh}{a+b}.
По условию задачи S_{KLMN}=\frac{3}{8}S_{ABCD}
, или
\frac{abh}{a+b}=\frac{3}{8}\cdot\frac{1}{2}(a+b)h,~\frac{ab}{a+b}=\frac{3}{8}\cdot\frac{1}{2}(a+b),
3a^{2}-10ab+3b^{2}=0,~3\left(\frac{a}{b}\right)^{2}-10\cdot\frac{a}{b}+3=0,
откуда находим, что \frac{a}{b}=3
или \frac{a}{b}=\frac{1}{3}
, а так как a\gt b
, то \frac{a}{b}=3
.
Источник: Вступительный экзамен в МФТИ. — 1965, билет 11, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 65-11-3, с. 112
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.39, с. 68
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.39.1, с. 72

