4574. В треугольнике ABC
биссектриса AD
делит сторону BC
в отношении BD:DC=2:1
. В каком отношении медиана CE
делит эту биссектрису?
Ответ. 3:1
, считая от вершины A
.
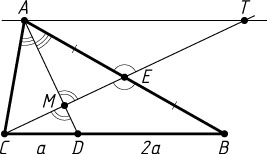
Решение. Пусть медиана CE
и биссектриса AD
пересекаются в точке M
. Через вершину A
проведём прямую, параллельную BC
и продолжим медиану CE
до пересечения с этой прямой в точке T
. Положим CD=a
, BD=2a
.
Из равенства треугольников AET
и BEC
следует, что AT=BC=3a
, а из подобия треугольников AMT
и DMC
— \frac{AM}{MD}=\frac{AT}{CD}=\frac{3a}{a}=3
.
