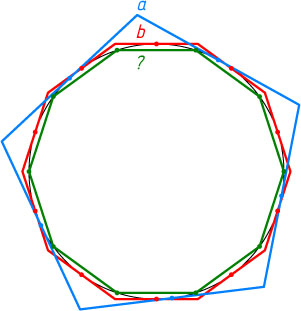
4576. Два правильных многоугольника с периметрами a
и b
описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют вдвое больше сторон, чем первый. Найдите периметр третьего многоугольника.
Ответ. \frac{b\sqrt{a}}{\sqrt{2a-b}}
.
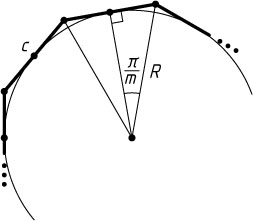
Решение. Заметим, что если c
— сторона правильного m
-угольника, описанного около окружности радиуса R
, то c=2R\tg\frac{\pi}{m}
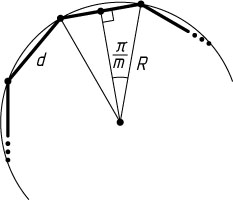
(рис. 1), а если d
— сторона правильного m
-угольника вписанного в окружность радиуса R
, то d=2R\sin\frac{\pi}{m}
(рис. 2).
Пусть R
— радиус окружности, x
— периметр третьего многоугольника, n
— число сторон первого многоугольника. Тогда 2n
— число сторон второго и третьего,
\frac{a}{n}=2R\tg\frac{\pi}{n},~\frac{b}{2n}=2R\tg\frac{\pi}{2n},~\frac{x}{2n}=2R\sin\frac{\pi}{2n}.
Из второго равенства следует, что 4nR=\frac{b}{\tg\frac{\pi}{2n}}
. Разделив почленно первое из этих равенств на второе, получим что
\frac{2a}{b}=\frac{\tg\frac{\pi}{n}}{\tg\frac{\pi}{2n}},~\frac{2a}{b}=\frac{\frac{2\tg\frac{\pi}{2n}}{1-\tg^{2}\frac{\pi}{2n}}}{\tg\frac{\pi}{2n}},~\frac{a}{b}=\frac{1}{1-\tg^{2}\frac{\pi}{2n}},
откуда \tg\frac{\pi}{2n}=\sqrt{\frac{a-b}{a}}
. Тогда
\cos\frac{\pi}{2n}=\frac{1}{\sqrt{1+\tg^{2}\frac{\pi}{2n}}}=\frac{1}{\sqrt{1+\frac{a-b}{a}}}=\frac{\sqrt{a}}{\sqrt{2a-b}}.
Следовательно,
x=4nR\cdot\sin\frac{\pi}{2n}=\frac{b}{\tg\frac{\pi}{2n}}\cdot\sin\frac{\pi}{2n}=b\cos\frac{\pi}{2n}=\frac{b\sqrt{a}}{\sqrt{2a-b}}.
Источник: Вступительный экзамен в МФТИ. — 1964, билет 1, № 2.


