4577. В полукруг радиуса R
вписаны два круга, касающиеся друг друга, полукруга и его диаметра. Радиус одного из них равен r
. Найдите радиус другого.
Ответ. \frac{rR(3R-2r\pm2\sqrt{2R(R-2r)})}{(R+2r)^{2}}
.
Решение. Пусть O
— центр полукруга, O_{1}
— центр круга радиуса r
, O_{2}
— центр круга неизвестного радиуса x
, M
и N
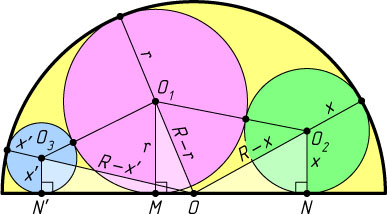
— точки касания соответственно первого и второго круга с диаметром полукруга. Тогда
O_{1}M=r,~O_{2}N=x,~O_{1}O_{2}=r+x,~MN=2\sqrt{xr},~OO_{1}=R-r,~OO_{2}=R-x
(см. задачу 365). Из прямоугольных треугольников OMO_{1}
и ONO_{2}
находим, что
OM=\sqrt{OO_{1}^{2}-O_{1}M^{2}}=\sqrt{(R-r)^{2}-r^{2}}=\sqrt{R^{2}-2Rr},
ON=\sqrt{OO_{2}^{2}-O_{2}N^{2}}=\sqrt{(R-x)^{2}-x^{2}}=\sqrt{R^{2}-2Rx},
Поскольку MN=|OM\pm ON|
, то
2\sqrt{xr}=|\sqrt{R^{2}-2rR}\pm\sqrt{R^{2}-2Rx}|.
Далее имеем:
\pm2\sqrt{xr}=\sqrt{R^{2}-2rR}\pm\sqrt{R^{2}-2xR}~\Rightarrow~\pm2\sqrt{xr}\pm\sqrt{R^{2}-2xR}=\sqrt{R^{2}-2rR}~\Rightarrow
\Rightarrow~(2\sqrt{xr}\pm\sqrt{R^{2}-2xR})^{2}=R^{2}-2rR~\Rightarrow~4xr+R^{2}-2xR\pm4\sqrt{xr(R^{2}-2xR)}=R^{2}-2rR~\Rightarrow
\Rightarrow~\pm2\sqrt{xr(R^{2}-2xR)}=rR-(R-2r)x~\Rightarrow~4xr(R^{2}-2xR)=(rR-(R-2r)x)^{2}~\Rightarrow
\Rightarrow~(R+2r)^{2}x^{2}-2rR(3R-2r)x+r^{2}R^{2}=0~\Rightarrow~x=\frac{rR(3R-2r\pm2\sqrt{2R(R-2r)})}{(R+2r)^{2}}.
Источник: Вступительный экзамен в МФТИ. — 1962, билет 10, № 4, 1964, билет 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 62-10-4, с. 103
