4578. В окружность вписаны три правильных многоугольника, число сторон каждого последующего вдвое больше, чем у предыдущего. Площади первых двух равны S_{1}
и S_{2}
. Найдите площадь третьего.
Ответ. \frac{S_{2}\sqrt{2S_{2}}}{\sqrt{S_{1}+S_{2}}}
.
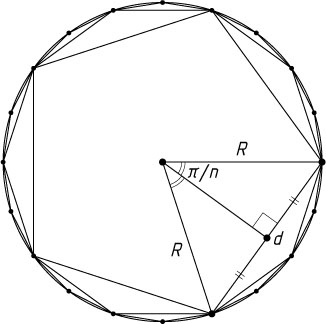
Решение. Заметим, что если d
— сторона правильного m
-угольника вписанного в окружность радиуса R
, то d=2R\sin\frac{\pi}{m}
.
Пусть S
— площадь третьего многоугольника, R
— радиус окружности, n
— число сторон первого многоугольника. Тогда 2n
— число сторон второго, 4n
— число сторон третьего,
S_{1}=n\cdot\frac{1}{2}R^{2}\sin\frac{2\pi}{n}=\frac{1}{2}nR^{2}\sin\frac{2\pi}{n},~S_{2}=2n\cdot\frac{1}{2}R^{2}\sin\frac{2\pi}{2n}=nR^{2}\sin\frac{\pi}{n}.
Разделив почленно первое из этих равенств на второе, получим, что
\frac{S_{1}}{S_{2}}=\frac{\sin\frac{2\pi}{n}}{2\sin\frac{\pi}{n}}=\cos\frac{\pi}{n},
а из второго равенства следует, что
nR^{2}=\frac{S_{2}}{\sin\frac{\pi}{n}}.
Следовательно,
S=4n\cdot\frac{1}{2}R^{2}\sin\frac{\pi}{2n}=2nR^{2}\cdot\sin\frac{\pi}{2n}=2\cdot\frac{S_{2}}{\sin\frac{\pi}{n}}\cdot\sin\frac{\pi}{2n}=\frac{2S_{2}\sin\frac{\pi}{2n}}{\sin\frac{\pi}{n}}=
=\frac{2S_{2}\sin\frac{\pi}{2n}}{2\sin\frac{\pi}{2n}\cos\frac{\pi}{2n}}=\frac{S_{2}}{\cos\frac{\pi}{2n}}=\frac{S_{2}}{\sqrt{\frac{1+\cos\frac{\pi}{n}}{2}}}=\frac{S_{2}}{\sqrt{\frac{1+\frac{S_{1}}{S_{2}}}{2}}}=\frac{S_{2}\sqrt{2S_{2}}}{\sqrt{S_{1}+S_{2}}}.
Источник: Вступительный экзамен в МФТИ. — 1964, билет 3, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 64-3-2, с. 103
