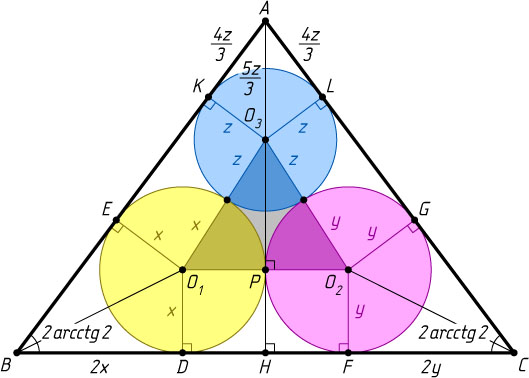
4585. Угол при основании равнобедренного треугольника равен 2\arcctg2
. Внутри треугольника расположены три окружности так, что каждая из них касается двух других окружностей и двух сторон треугольника. Найдите отношение радиусов этих окружностей.
Ответ. 1:1:\frac{2(3+\sqrt{5})}{9}
.
Решение. Пусть окружность радиуса x
с центром O_{1}
касается основания BC
равнобедренного треугольника ABC
в точке D
, а боковой стороны AB
— в точке E
; окружность радиуса y
с центром O_{2}
касается основания BC
в точке F
, а боковой стороны AC
— в точке G
; окружность радиуса z
с центром O_{3}
касается боковых сторон AB
и AC
в точках K
и L
соответственно.
Из прямоугольных треугольников BO_{1}D
, CO_{2}F
и AO_{3}K
находим, что
BD=O_{1}D\ctg\frac{1}{2}\angle ABC=x\ctg(\arcctg2)=2x,
CF=O_{2}F\ctg\frac{1}{2}\angle ACB=y\ctg(\arcctg2)=2y.
AK=O_{3}K\tg\angle AO_{3}K=O_{3}K\tg\angle ABC=
=O_{3}K\tg(2\arcctg2)=
=O_{3}K\tg\left(2\arctg\frac{1}{2}\right)=z\cdot\frac{2\cdot\frac{1}{2}}{1-\frac{1}{4}}=\frac{4}{3}z,
AO_{3}=\sqrt{AK^{2}+O_{3}K^{2}}=\sqrt{\frac{16}{9}z^{2}+z^{2}}=\frac{5}{3}z.
Тогда
AB=AK+KE+BE=AK+KE+BD=\frac{4}{3}z+2\sqrt{xz}+2x
(см. задачу 365),
AC=AL+LG+CG=AK+LG+CF=\frac{4}{3}z+2\sqrt{yz}+2y,
а так как AB=AC
, то
\frac{4}{3}z+2\sqrt{xz}+2x=\frac{4}{3}z+2\sqrt{yz}+2y,~2\sqrt{xz}+2x=2\sqrt{yz}+2y,
\sqrt{xz}+x=\sqrt{yz}+y,~\sqrt{xz}-\sqrt{yz}+x-y=0,
\sqrt{z}(\sqrt{x}-\sqrt{y})+(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})=0,~(\sqrt{x}-\sqrt{y})(\sqrt{z}+\sqrt{x}+\sqrt{y})=0,
откуда следует, что x=y
, значит, окружности с центрами O_{1}
и O_{2}
равны. Тогда высота AH
равнобедренного треугольника ABC
проходит через точку P
касания этих окружностей, а O_{3}P
— высота равнобедренного треугольника O_{1}O_{2}O_{3}
с основанием O_{1}O_{2}=2x
и боковыми сторонами O_{1}O_{3}=O_{2}O_{3}=x+z
.
Из прямоугольного треугольника AHB
находим, что
AH=BH\tg\angle ABC=(BD+DH)\tg\left(2\arctg\frac{1}{2}\right)=(2x+x)\cdot\frac{4}{3}=4x.
В прямоугольном треугольнике O_{3}O_{1}P
известно, что
O_{3}P=AH-AO_{3}-PH=4x-\frac{5}{3}z-x=3x-\frac{5}{3}z,~O_{1}P=x,~O_{1}O_{3}=x+z,
причём x\gt\frac{5}{9}z
, так как 3x-\frac{5}{3}z\gt0
. По теореме Пифагора
O_{3}P^{2}+O_{1}P^{2}=O_{1}O_{3}^{2},~\left(3x-\frac{5}{3}z\right)^{2}+x^{2}=(x+z)^{2},~9x^{2}-12xz+\frac{16}{9}z^{2}=0,
откуда \frac{x}{z}=\frac{2(3\pm\sqrt{5})}{9}
, а так как \frac{x}{z}\gt\frac{5}{9}
, то \frac{x}{z}=\frac{2(3+\sqrt{5})}{9}
.
Источник: Вступительный экзамен в МФТИ. — 1963, билет 4, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 63-4-4, с. 98
