4587. Все вершины правильного треугольника лежат на сторонах прямоугольного треугольника. Одна из сторон правильного треугольника параллельна гипотенузе и длина её в три раза меньше длины гипотенузы. Найдите углы прямоугольного треугольника.
Ответ. 30^{\circ}
, 60^{\circ}
.
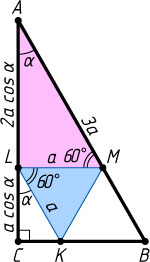
Решение. Пусть вершины K
и L
правильного треугольника KLM
лежат на катетах соответственно BC
и AC
прямоугольного треугольника ABC
, а вершина M
— на гипотенузе AB
. Обозначим \angle BAC=\alpha
, KL=a
. Тогда
\angle KLC=\angle BAC=\alpha,~AB=3a,~AC=AB\cos\alpha=3a\cos\alpha,
LC=a\cos\alpha,~AL=AC-LC=2a\cos\alpha,~\angle AML=\angle KLM=60^{\circ}.
Применяя теорему синусов к треугольнику AML
, получим, что
\frac{ML}{\sin\angle MAL}=\frac{AL}{\sin\angle AML},~\frac{a}{\sin\alpha}=\frac{2a\cos\alpha}{\sin60^{\circ}},~2\sin\alpha\cos\alpha=\frac{\sqrt{3}}{2},~\sin2\alpha=\frac{\sqrt{3}}{2},
откуда 2\alpha=60^{\circ}
или 2\alpha=120^{\circ}
. Следовательно, \alpha=30^{\circ}
или \alpha=60^{\circ}
.
Источник: Вступительный экзамен в МФТИ. — 1963, билет 6, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 63-6-2, с. 99
