4592. Длина внешней касательной окружностей радиусов r
и R
в два раза больше длины внутренней касательной. Найдите расстояние между центрами этих окружностей.
Ответ. \sqrt{R^{2}+r^{2}+\frac{10}{3}rR}
.
Решение. Пусть O_{1}
и O_{2}
— центра окружностей радиусов r
и R
соответственно, AB
— общая внешняя касательная этих окружностей, CD
— общая внутренняя касательная (точки A
и C
лежат на первой окружности, B
и D
— на второй), AB=2CD
.
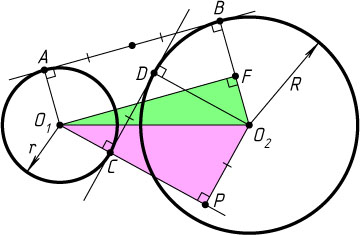
Опустим перпендикуляры O_{1}F
и O_{2}P
из центров O_{1}
и O_{2}
окружностей на прямые O_{2}B
и O_{1}C
соответственно. Тогда
AB=O_{1}F,~CD=O_{2}P,~O_{2}F=R-r,~O_{1}P=R+r.
Из прямоугольных треугольников O_{1}FO_{2}
и O_{1}PO_{2}
находим, что
AB^{2}=O_{1}F^{2}=O_{1}O_{2}^{2}-O_{2}F^{2}=O_{1}O_{2}^{2}-(R-r)^{2},
CD^{2}=O_{2}P^{2}=O_{1}O_{2}^{2}-O_{1}P^{2}=O_{1}O_{2}^{2}-(R+r)^{2},
а так как AB^{2}=4CD^{2}
, получим уравнение
O_{1}O_{2}^{2}-(R-r)^{2}=4O_{1}O_{2}^{2}-4(R+r)^{2},
из которого находим, что
O_{1}O_{2}^{2}=\frac{1}{3}(4(R+r)^{2}-(R-r)^{2})=R^{2}+\frac{10}{3}rR+r^{2}.
Следовательно,
O_{1}O_{2}=\sqrt{R^{2}+r^{2}+\frac{10}{3}rR}.
Источник: Вступительный экзамен в МФТИ. — 1963, билет 12, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 63-12-3, с. 102
