4595. На высоте правильного треугольника, сторона которого равна b
, как на диаметре построена окружность. Найдите площадь той части треугольника, которая лежит внутри окружности.
Ответ. \frac{b^{2}(2\pi+3\sqrt{3})}{32}
.
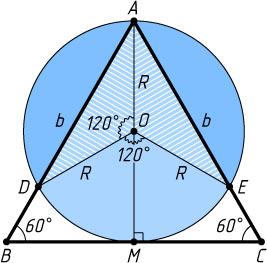
Решение. Пусть окружность с центром O
радиуса R
, построенная на высоте AM
равностороннего треугольника ABC
, пересекает стороны AB
и AC
в точках D
и E
соответственно. Тогда
R=\frac{1}{2}AM=\frac{b\sqrt{3}}{4},~OE=OM=OD=R,~\angle EOD=2\angle DAE=120^{\circ}.
Пусть S_{1}
— площадь сектора DOE
, S_{2}
— площадь круга радиуса R
, S
— искомая площадь части треугольника, заключённой внутри окружности. Тогда
S_{2}=\pi R^{2},~S_{1}=\frac{1}{3}S_{2}=\frac{1}{3}\pi R^{2}.
Следовательно,
S=S_{1}+2S_{\triangle AOD}=\frac{1}{3}\pi R^{2}+2\cdot\frac{1}{2}R^{2}\sin\angle AOD=
=\frac{1}{3}\pi R^{2}+R^{2}\sin60^{\circ}=\frac{1}{3}\pi R^{2}+\frac{R^{2}\sqrt{3}}{2}=\frac{1}{6}R^{2}(2\pi+3\sqrt{3})=
=\frac{1}{6}\cdot\left(\frac{b\sqrt{3}}{4}\right)^{2}\cdot(2\pi+3\sqrt{3})=\frac{b^{2}(2\pi+3\sqrt{3})}{32}.
Источник: Вступительный экзамен в МФТИ. — 1962, билет 4, № 1.
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 62-4-1, с. 91
