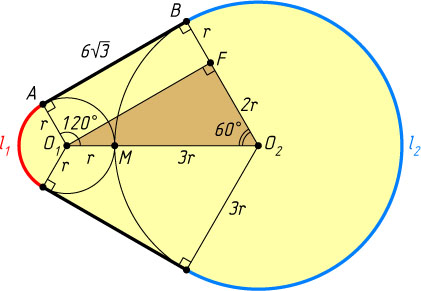
4605. Две окружности касаются внешним образом. Их радиусы относятся как 3:1
, а длина их общей внешней касательной равна 6\sqrt{3}
. Найдите периметр фигуры, образованной внешними касательными и внешними частями окружностей.
Ответ. 14\pi+12\sqrt{3}
.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и 3r
соответственно, M
— точка касания окружностей, AB
— общая внешняя касательная этих окружностей (точка A
лежит на первой окружности, B
— на второй).
Опустим перпендикуляр O_{1}F
из центра первой окружности на радиус O_{2}B
второй окружности. В прямоугольном треугольнике O_{1}O_{2}F
известно, что
O_{1}O_{2}=O_{1}M+O_{2}M=r+3r=4r,
O_{2}F=O_{2}B-BF=O_{2}F-O_{1}A=3r-r=2r,
поэтому
\angle FO_{2}O_{1}=60^{\circ},~\angle AO_{1}O_{2}=120^{\circ},~AB=O_{1}F=2r\sqrt{3}=6\sqrt{3},
откуда r=3
, 3r=9
.
Пусть P
— периметр искомой фигуры, l_{1}
и l_{2}
— длины внешних частей первой и второй окружностей соответственно.
l_{1}=\frac{1}{3}\cdot2\pi r=\frac{1}{3}\cdot2\pi\cdot3=2\pi,~l_{2}=\frac{2}{3}\cdot2\pi\cdot3r=\frac{2}{3}\cdot2\pi\cdot9=12\pi
Следовательно,
P=2AB+l_{1}+l_{2}=12\sqrt{3}+14\pi.