4623. Касательные, проведённые к вписанной окружности треугольника ABC
, отсекают от него треугольники: первый — с вершиной A
, второй — с вершиной B
, третий — с вершиной C
. Докажите, что сумма периметров отсечённых треугольников равна периметру треугольника ABC
.
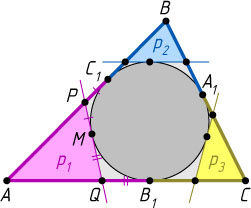
Решение. Пусть вписанная окружность касается сторон AB
, AC
и BC
треугольника ABC
в точках C_{1}
, B_{1}
и A_{1}
соответственно, а прямая касается вписанной окружности треугольника ABC
в точке M
и пересекает стороны AB
и AC
соответственно в точках P
и Q
. Тогда PM=PC_{1}
и QM=QB_{1}
, значит,
AP+PQ+AQ=AP+(PM+MQ)+AQ=(AP+PM)+(MQ+AQ)=
=(AP+PC_{1})+(QB_{1}+AQ)=AC_{1}+AB_{1},
т. е. периметр p_{1}
первого отсечённого треугольника равен AC_{1}+AB_{1}
. Аналогично периметр p_{2}
второго отсечённого треугольника равен BC_{1}+BA_{1}
, а периметр p_{3}
третьего — CA_{1}+CB_{1}
. Следовательно,
p=AB+BC+AC=(AC_{1}+BC_{1})+(BA_{1}+CA_{1})+(CB_{1}+AB_{1})=
=(AC_{1}+AB_{1})+(BC_{1}+BA_{1})+(CA_{1}+CB_{1})=p_{1}+p_{2}+p_{3}.
Что и требовалось доказать.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 95, с. 39
