4627. Две окружности радиусов R
и r
касаются внешним образом. Найдите площадь трапеции, образованной общими внешними касательными к этим окружностям и хордами, соединяющими точки касания.
Ответ. \frac{8Rr\sqrt{Rr}}{R+r}
.
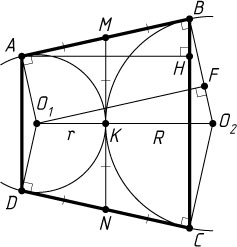
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно (r\lt R)
, AB
и CD
— общие внешние касательные к этим окружностям (точки A
и D
расположены на меньшей окружности, точки B
и C
— на большей), K
— точка касания окружностей, F
— проекция точки O_{1}
на O_{2}B
, H
— проекция точки A
на BC
.
Линия центров двух касающихся окружностей проходит через точку их касания, поэтому O_{1}O_{2}=O_{1}K+KO_{2}=r+R
. Четырёхугольник ABFO_{1}
— прямоугольник, поэтому
AB=O_{1}F=\sqrt{O_{1}O_{2}^{2}-O_{2}F^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{Rr}.
Прямоугольные треугольники O_{1}FO_{2}
и AHB
подобны, так как \angle FO_{1}O_{2}=\angle HAB
, значит, \frac{AH}{O_{1}F}=\frac{AB}{O_{1}O_{2}}
, откуда находим, что
AH=O_{1}F\cdot\frac{AB}{O_{1}O_{2}}=2\sqrt{Rr}\cdot\frac{2\sqrt{Rr}}{R+r}=\frac{4Rr}{R+r}.
Пусть общая касательная, проведённая через точку K
пересекает отрезки AB
и CD
в точках M
и N
соответственно. Тогда
AM=MK=MB,~ND=NK=NC,
значит, M
и N
— середины боковых сторон AB
и CD
равнобедренной трапеции ABCD
с высотой AH
, а
MN=MK+KN=\frac{1}{2}AB+\frac{1}{2}CD=\frac{1}{2}(2\sqrt{Rr}+2\sqrt{Rr})=2\sqrt{Rr}
— средняя линия трапеции. Следовательно,
S_{ABCD}=MN\cdot AH=2\sqrt{Rr}\cdot\frac{4Rr}{R+r}=\frac{8Rr\sqrt{Rr}}{R+r}.
Источник: Вступительный экзамен в МФТИ. — 1969, билет 4, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 69-4-3, с. 132
